A triangular pyramid, also called a tetrahedron, is a pyramid where the base is a triangle. The figure therefore has a total of four faces, all of which are triangles.

 

The tetrahedron is the simplest type of pyramid and one of the five Platonic solids. If all edges are equal, all faces are equilateral triangles, and the tetrahedron is regular.

 

 

 

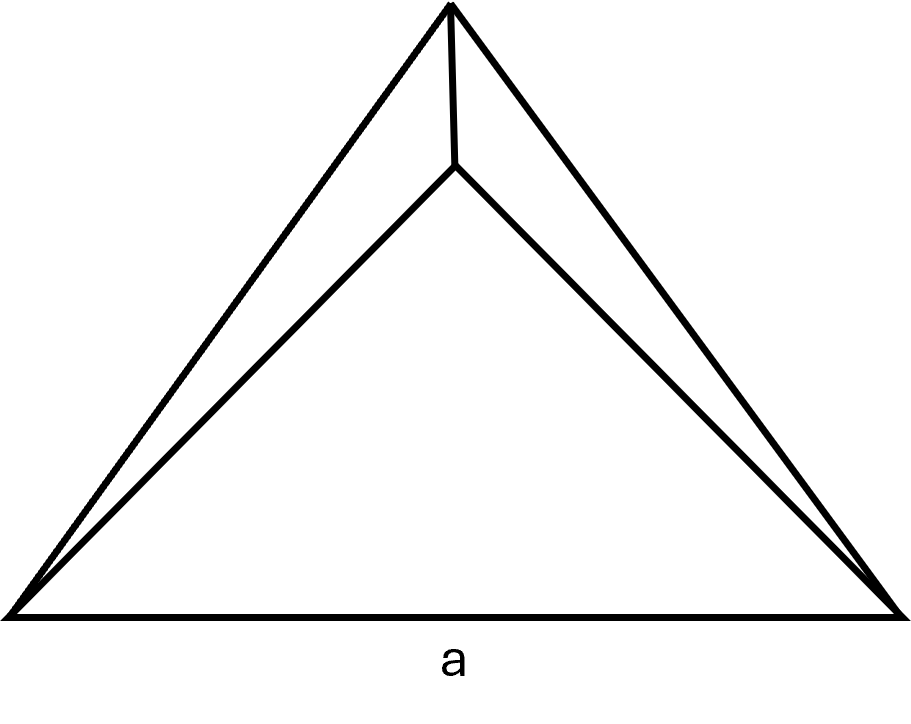
Regular triangular pyramid (tetrahedron)

 

 

Volume

The volume of a triangular pyramid is found using the general pyramid formula:

 

$$ \large V = \frac{1}{3} \cdot A_{base} \cdot h $$

 

If the pyramid is a regular tetrahedron with side length \( \large a \), the volume can be written as:

 

$$ \large V = \frac{a^3}{6 \cdot \sqrt{2}} $$

 

 

Surface area

The surface area consists of the base and the three triangular side faces:

 

$$ \large S = A_{base} + A_{sides} $$

 

For a regular tetrahedron, where all four triangles are equilateral with side length \( \large a \), this becomes:

 

$$ \large S = \sqrt{3} \cdot a^2 $$

 

 

Irregular triangular pyramid

An irregular triangular pyramid has an arbitrary triangle as its base, or the apex is not symmetric, or the edges have different lengths.

 

 

 

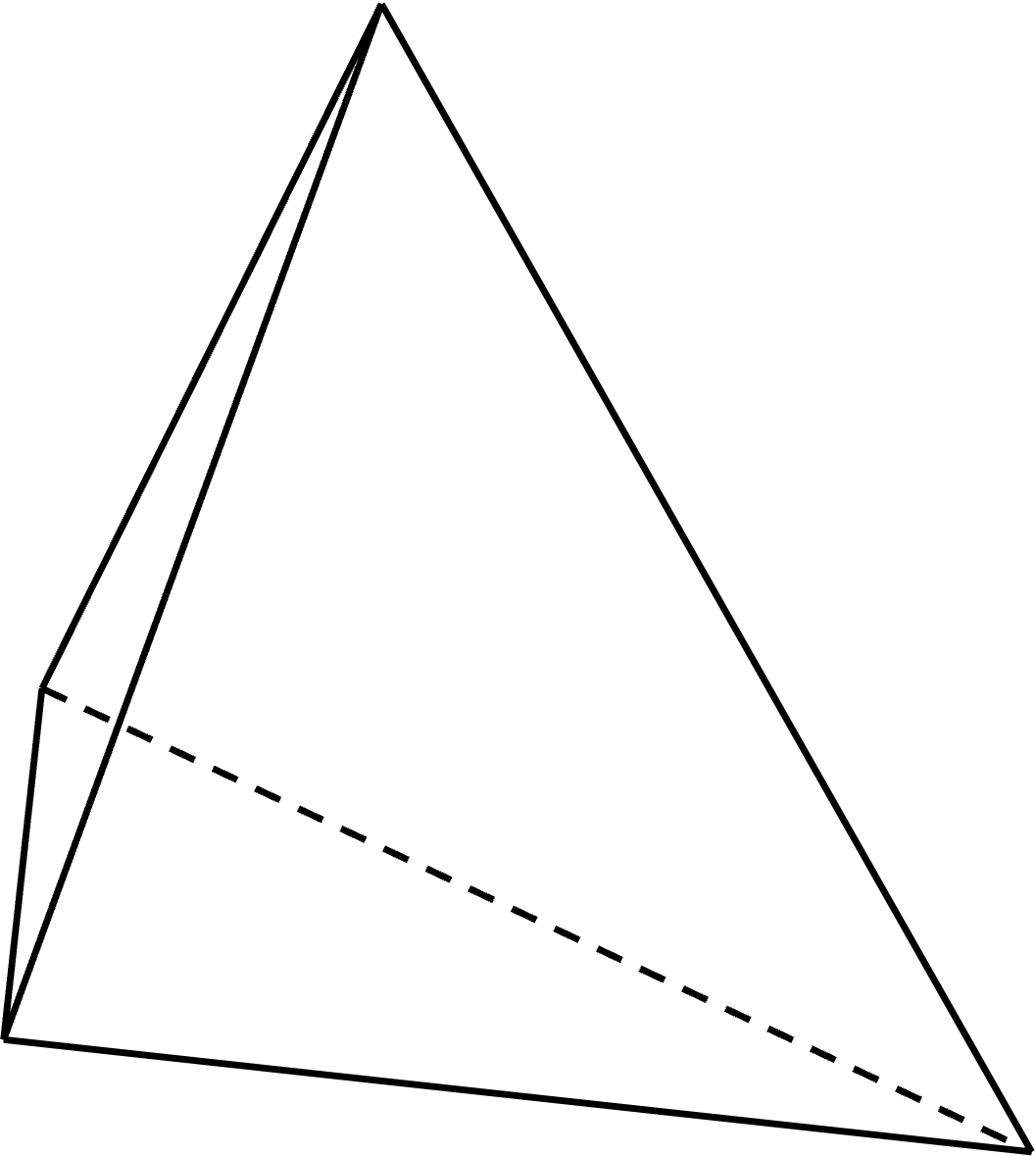
If the triangular base is right-angled and twice as tall as it is wide, then the 3 edges in the base cannot be equal in length, which means the pyramid cannot be a regular tetrahedron.

It is still a triangular pyramid, but not a regular tetrahedron.

 

For irregular triangular pyramids, the general formulas for pyramids apply.

However, the calculation of the areas of the base and the side faces requires individual methods, e.g. Heron’s formula for triangles.

 

 

Heron’s formula

To calculate the area of an arbitrary triangular base, one can use Heron’s formula. If the triangle has side lengths \( \large a \), \( \large b \), \( \large c \), and the semiperimeter is:

 

$$ \large s = \frac{a+b+c}{2} $$

 

the area is:

 

$$ \large A = \sqrt{s \cdot (s-a) \cdot (s-b) \cdot (s-c)} $$