A pyramid is a solid figure consisting of a polygon as a base and an apex to which all the vertices of the base are connected. The faces that appear between the apex and the sides of the base are triangles and are called lateral faces.

 

The height of a pyramid is the perpendicular distance from the apex to the plane of the base. If the pyramid is right, the apex is exactly above the center of the base.

 

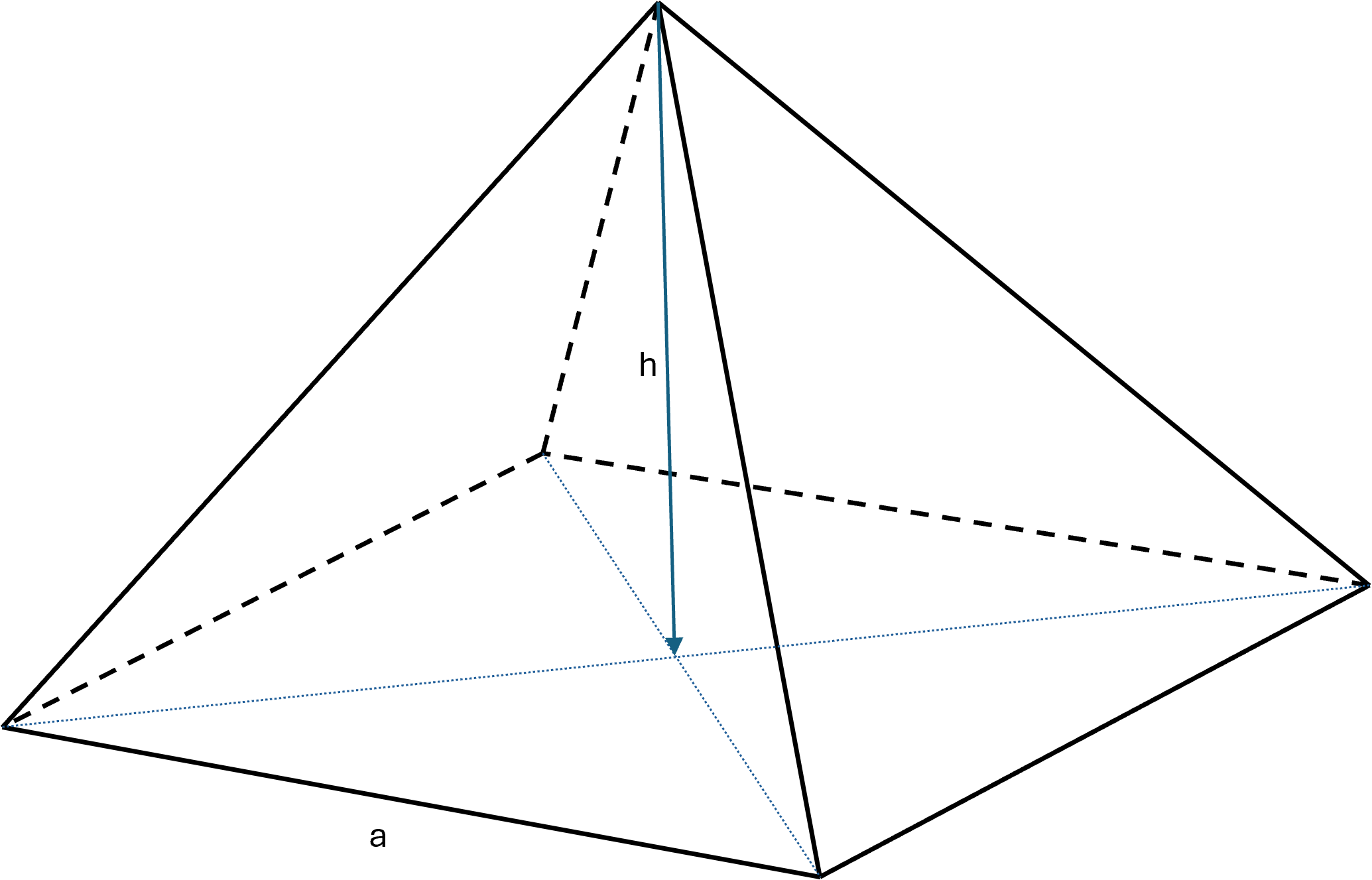
Right pyramid with square base

 

If the pyramid is oblique, the apex is not above the center of the base.

 

 

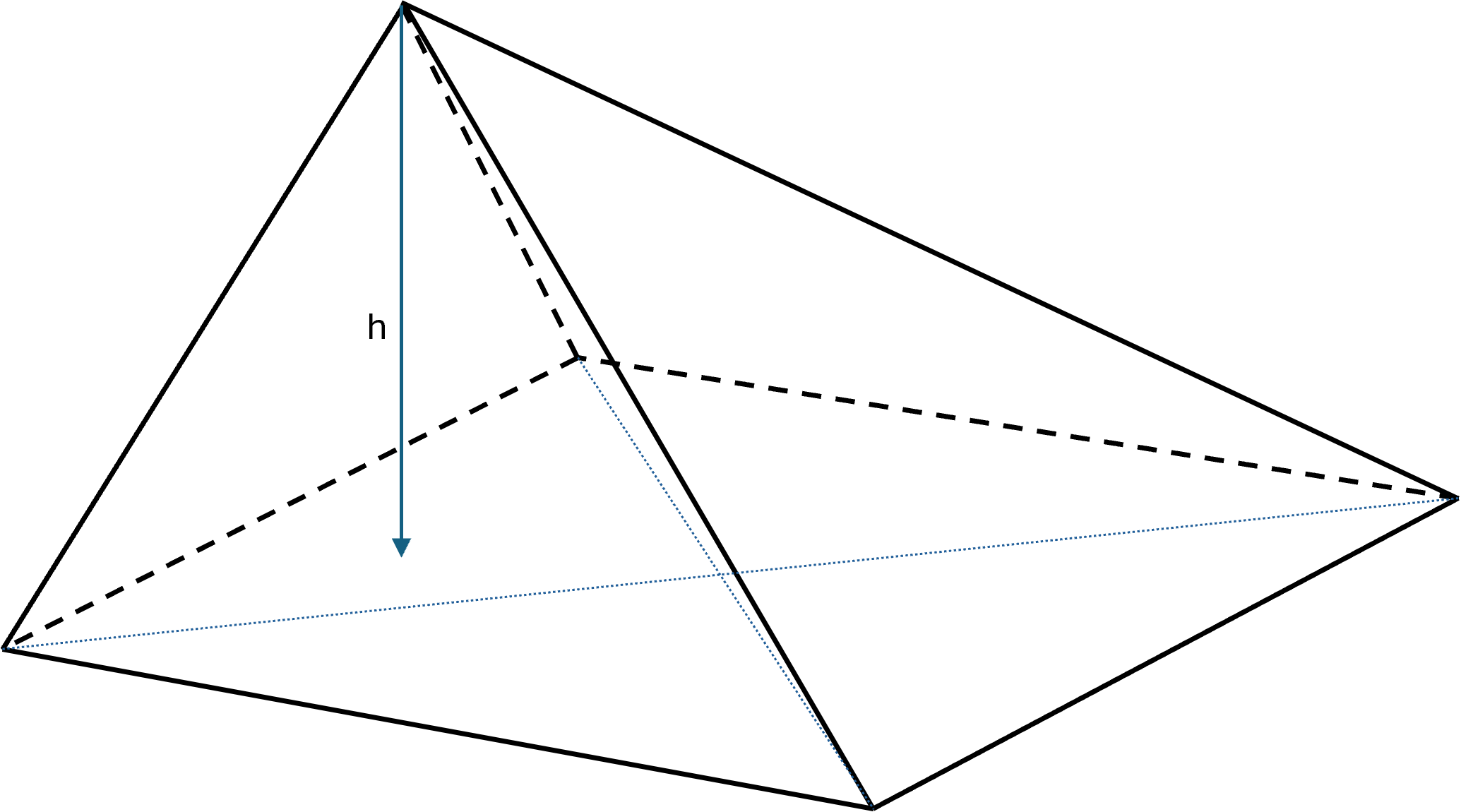
Oblique pyramid with square base

 

 

Volume

The volume of a pyramid is always one third of the area of the base multiplied by the height:

 

$$ \large V = \frac{1}{3} \cdot A_{base} \cdot h $$

 

 

Surface area

The surface area consists of the base and the triangular lateral faces:

 

$$ \large S = A_{base} + \sum_{i=1}^{n} A_i $$

 

Where \( A_i \) is the area of each triangular lateral face. For regular pyramids, the formula can be simplified since all lateral faces are equal.

 

 

Types of pyramids

Just like the prism, a pyramid can have different bases:

• Triangular pyramid (tetrahedron): The base is a triangle.
• Square pyramid: The base is a quadrilateral, often a square (known from the Egyptian pyramids).
• Pentagonal, hexagonal, ... n-gonal pyramid: The base can be any polygon.

 

Comparison with prism

A pyramid always has one third of the volume of a prism with the same base and the same height. This relationship explains the volume formula:

 

$$ \large V_{\text{pyramid}} = \frac{1}{3} \cdot V_{\text{prism}} $$