A pyramid frustum is the solid figure obtained when the top of a right pyramid is cut off with a plane parallel to the base.

 

The figure therefore has two parallel polygonal bases, a smaller one and a larger one, as well as several trapezoidal side faces. The number of side faces depends on the number of sides of the base.

 

 

 

 

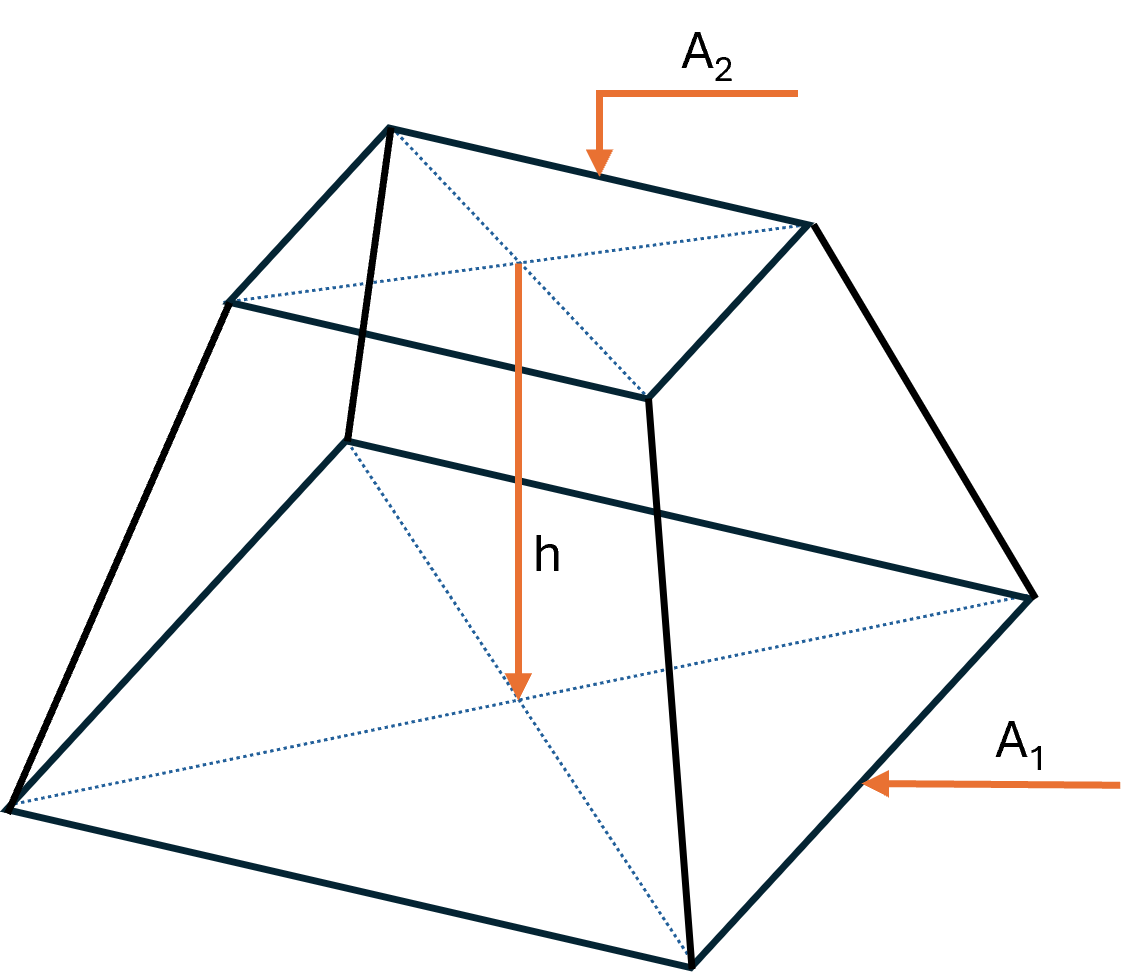
Volume

The volume of a pyramid frustum with height \( \large h \), large base area \( \large A_{1} \) and small base area \( \large A_{2} \) is:

 

$$ \large V = \frac{1}{3} \cdot h \cdot \left(A_{1} + A_{2} + \sqrt{A_{1} \cdot A_{2}}\right) $$

 

This formula applies generally for all pyramid frustums, regardless of the number of sides of the base.

 

 

Surface area

The surface area consists of the two parallel bases as well as the trapezoidal side faces. The side faces are usually not identical, and each must be calculated from the height, the edge lengths and the slant heights.

 

For a square pyramid frustum there are four trapezoidal side faces, while a pentagonal pyramid frustum has five, and so on. In principle there are infinitely many variations.

 

 

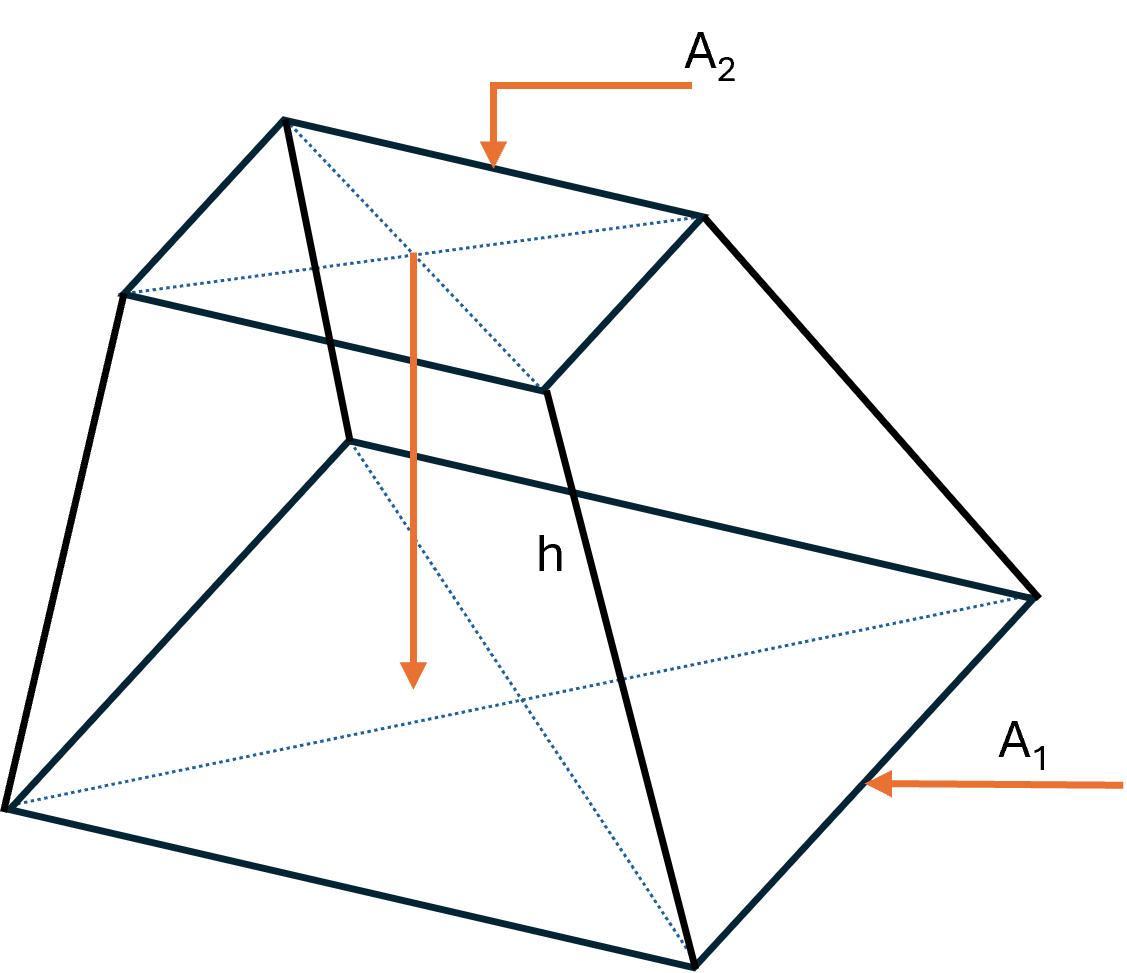
Irregular pyramid frustum

An irregular pyramid frustum arises when an irregular pyramid is cut with a plane parallel to the base.

The two bases remain parallel, but their centers are offset and the side faces are slanted.

 

 

 

 

Truncated pyramid

If a pyramid is cut with a plane that is not parallel to the base, one obtains a truncated pyramid. In this case the top face is no longer a copy of the base, but another polygon.

 

 

 

 

The volume can still be calculated using integral calculus, but there are no simple closed formulas for the surface area as in the case of the right pyramid frustum.