Trapezoidal rule

The trapezoidal rule is a simple numerical method for calculating an approximate value of a definite integral. It is based on the idea of replacing the graph of a function with straight lines so that the area under the curve can be computed as the sum of trapezoids.

 

 

The idea behind the method

When the exact integral \( \large \int_a^b f(x)\,dx \) cannot be found, the interval \( \large [a,b] \) can instead be divided into \( \large n \) smaller subintervals. On each subinterval, the function is replaced by a straight line between the two endpoints. The area under this line is a trapezoid, which is easy to compute.

 

 

Formula for the trapezoidal rule

For an interval divided into \( \large n \) equal parts with width \( \large h = \frac{b-a}{n} \), we have:

 

$$ \large \int_a^b f(x)\,dx \approx \frac{h}{2} \left[f(x_0) + 2f(x_1) + 2f(x_2) + \ldots + 2f(x_{n-1}) + f(x_n)\right] $$

 

 

Step-by-step procedure

 

1. Divide the interval \( \large [a,b] \) into \( \large n \) equal parts.
2. Compute \( \large h = \frac{b-a}{n} \).
3. Compute the function values \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
4. Insert the values into the trapezoidal formula.

 

 

Example

We will calculate the approximate area under the function \( \large f(x) = x^2 \) on the interval \( \large [0,2] \) using 4 trapezoids.

 

Here \( \large a = 0 \), \( \large b = 2 \), and \( \large n = 4 \), so \( \large h = \frac{2-0}{4} = 0{,}5 \).

 

The function values are:

 

$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$

 

The trapezoidal formula gives:

 

$$ \large A \approx \frac{0{,}5}{2}\,[0 + 2(0{,}25 + 1 + 2{,}25) + 4] = 2{,}75 $$

 

The exact integral is \( \large \int_0^2 x^2\,dx = \frac{8}{3} \approx 2{,}67 \), so the method provides a good approximation.

 

 

 

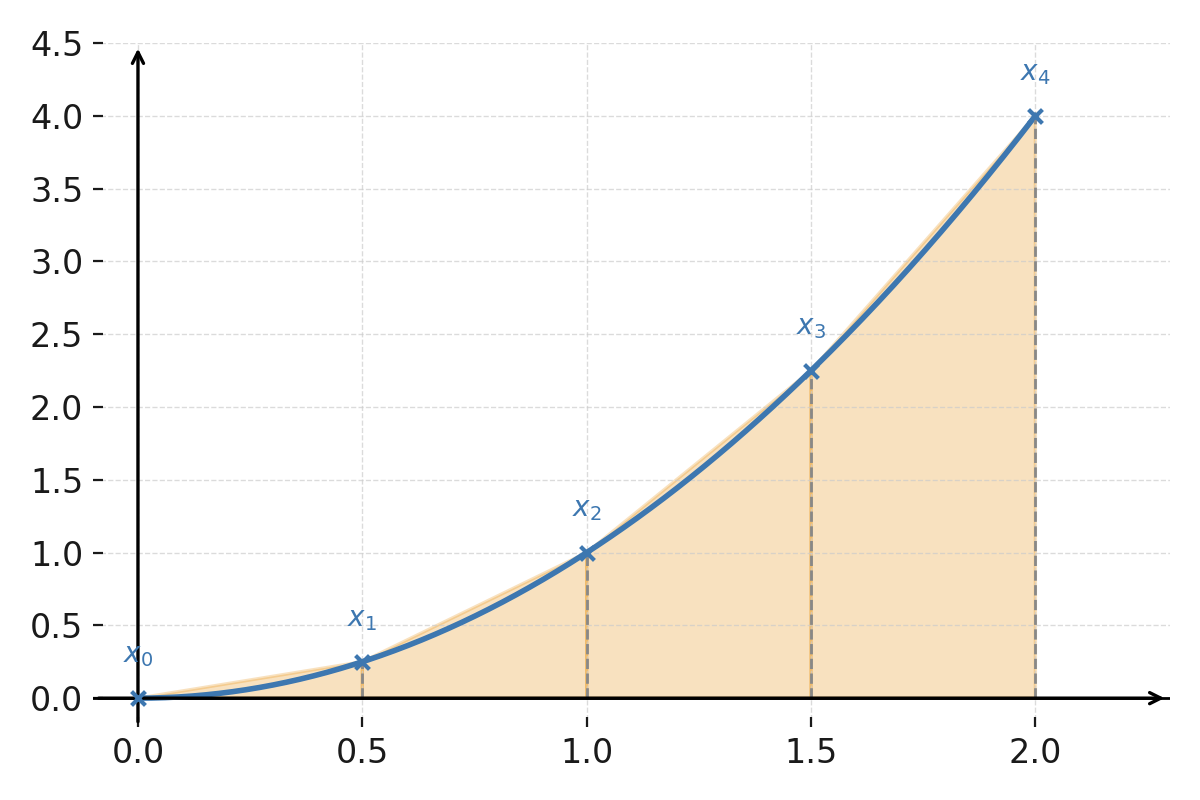
The function \( \large f(x) = x^2 \) on the interval \( \large [0,2] \).

The four subintervals are marked with vertical dashed lines, and the corresponding trapezoids are shown between the curve and the x-axis.

 

 

Remarks

The trapezoidal rule is easy to implement and often gives good accuracy, but it may underestimate or overestimate the area depending on whether the function is convex or concave. The accuracy can be improved by using more subintervals or by applying Simpson’s rule.