Simpson’s rule
Simpson’s rule is an improvement of the trapezoidal rule for numerically calculating a definite integral. While the trapezoidal rule replaces the function with straight lines, Simpson’s rule instead uses parabolas (quadratic polynomials) to approximate the curve. This provides much higher accuracy even with a few subintervals.
The idea behind the method
Suppose we want to calculate the area under the function \( \large f(x) \) between \( \large a \) and \( \large b \). The interval is divided into an even number of subintervals (for example \( \large n = 4 \)). On each pair of subintervals, a parabola is drawn through the three points \( \large (x_{2i}, f(x_{2i})) \), \( \large (x_{2i+1}, f(x_{2i+1})) \), and \( \large (x_{2i+2}, f(x_{2i+2})) \). The sum of the areas under these parabolas gives an approximation to the total integral.
Formula for Simpson’s rule
If \( \large n \) is an even number and the subinterval width is \( \large h = \frac{b-a}{n} \), then:
$$ \large \int_a^b f(x)\,dx \approx \frac{h}{3}\,[f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + \ldots + 4f(x_{n-1}) + f(x_n)] $$
Step-by-step procedure
- Divide the interval \( \large [a,b] \) into an even number of subintervals \( \large n \).
- Compute \( \large h = \frac{b-a}{n} \).
- Compute the function values \( \large f(x_0), f(x_1), \ldots, f(x_n) \).
- Insert the values into Simpson’s formula.
Example
We calculate the approximate area under \( \large f(x) = x^2 \) on the interval \( \large [0,2] \) with \( \large n = 4 \).
Here \( \large h = \frac{2-0}{4} = 0{,}5 \).
The function values are:
$$ \large f(0)=0, \quad f(0{,}5)=0{,}25, \quad f(1)=1, \quad f(1{,}5)=2{,}25, \quad f(2)=4 $$
Substituting into Simpson’s formula gives:
$$ \large A \approx \frac{0{,}5}{3}\,[0 + 4(0{,}25) + 2(1) + 4(2{,}25) + 4] = 2{,}67 $$
This corresponds exactly to the exact integral:
$$ \large \int_0^2 x^2\,dx = \frac{8}{3} = 2{,}67 $$
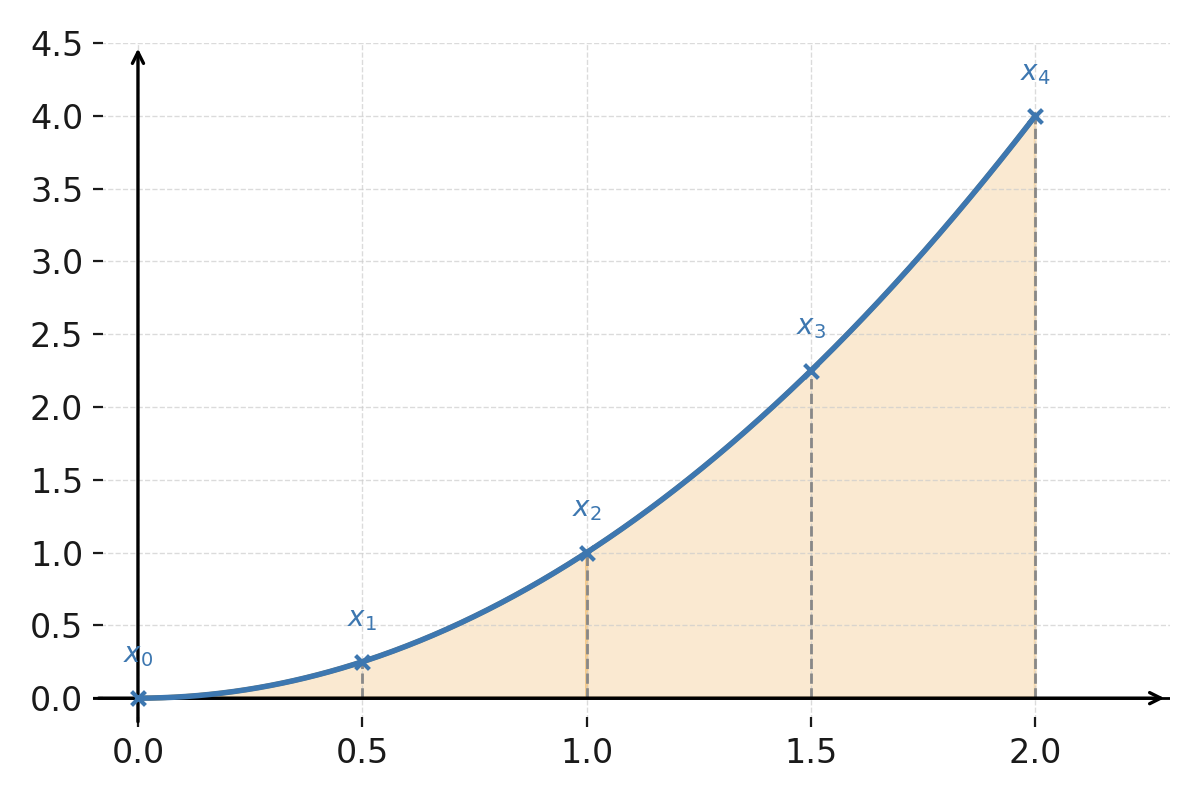
The function \( \large f(x)=x^2 \).
Over each pair of subintervals, a parabola approximates the function. The limits \( \large x_0, x_1, x_2, x_3, x_4 \) are marked with gray dashed lines.
Remarks
Simpson’s rule provides much higher accuracy than the trapezoidal rule because it accounts for the curvature of the function. However, it can only be applied when the number of subintervals \( \large n \) is even. When combined across several parabolas, the method is called the composite Simpson’s rule.