Bisection method

The bisection method is a simple numerical technique for finding a root in a continuous function, that is, a point where $ \large f(x) = 0 $.

The method is based on the intermediate value theorem, which states that if $ \large f(a) $ and $ \large f(b) $ have opposite signs, then there must exist at least one root in the interval $ \large [a,b] $.

The idea behind the method

The interval is repeatedly divided into two halves. At each step, it is determined in which half the function changes sign. That half is chosen as the new interval, and the process is repeated until the position of the root is known with the desired accuracy.

Step-by-step procedure

Choose a starting interval $ \large [a,b] $ where $ \large f(a) $ and $ \large f(b) $ have opposite signs.
Compute the midpoint $ \large m = \frac{a + b}{2} $.
Evaluate $ \large f(m) $.
If $ \large f(m) = 0 $ (or very close to 0), then $ \large m $ is the root.
Otherwise, if $ \large f(a) $ and $ \large f(m) $ have opposite signs, set $ \large b = m $; otherwise set $ \large a = m $.
Repeat steps 2–5 until the interval length is smaller than the chosen tolerance $ \large \varepsilon $.

Example

We want to find the root of the function $ \large f(x) = x^3 - x - 2 $.

We observe that $ \large f(1) = -2 $ and $ \large f(2) = 4 $, so the function changes sign in the interval $ \large [1,2] $.

$$ \large m_1 = \frac{1 + 2}{2} = 1{,}5 $$

$$ \large f(1{,}5) = (1{,}5)^3 - 1{,}5 - 2 $$

$$ \large f(1{,}5) = -0{,}125 $$

Because $ \large f(1{,}5) $ and $ \large f(2) $ have opposite signs, a new interval $ \large [1{,}5, 2] $ is chosen.

$$ \large m_2 = \frac{1{,}5 + 2}{2} = 1{,}75 $$

$$ \large f(1{,}75) = (1{,}75)^3 - 1{,}75 - 2 $$

$$ \large f(1{,}75) = 1{,}609 - 3{,}75 $$

$$ \large f(1{,}75) = -0{,}109 $$

The process continues until $ \large a $ and $ \large b $ are so close that the root can be read as $ \large x \approx 1{,}521 $.

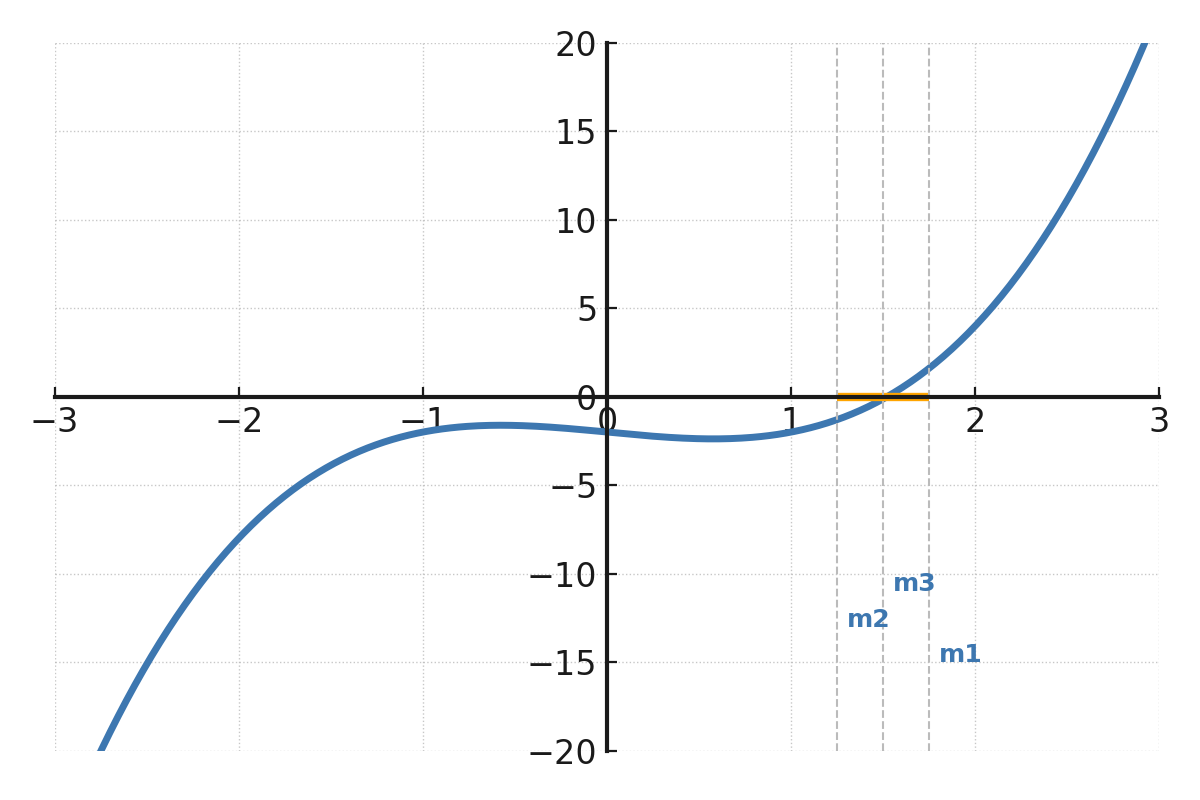
Bisection method

The function $ \large f(x) = x^3 - x - 2 $, where the interval $ \large [1,2] $ is shown as a line on the x-axis.

The midpoints $ \large m_1, m_2, m_3 $ appear as vertical lines that gradually approach the position of the root where the graph crosses the x-axis.

Note

The bisection method is very robust because it always converges if the function is continuous and changes sign. The drawback is that it converges slowly compared to more advanced methods such as Newton-Raphson.