Numerical differentiation

When no analytical formula for the function is available, the derivative \( \large f'(x) \) can be found using numerical methods. Numerical differentiation is based on approximating the slope of the tangent from discrete points instead of using the exact limit value.

 

 

The idea behind the method

The derivative at a point describes the local slope of the tangent to the function. If the function values are known at points that are close to each other, an approximate slope can be calculated between them. This is done using difference quotients.

 

 

Forward, backward, and central difference

There are three basic formulas for numerical differentiation:

 

Forward difference:

 

$$ \large f'(x) \approx \frac{f(x+h) - f(x)}{h} $$

 

Backward difference:

 

$$ \large f'(x) \approx \frac{f(x) - f(x-h)}{h} $$

 

Central difference:

 

$$ \large f'(x) \approx \frac{f(x+h) - f(x-h)}{2h} $$

 

The central difference usually gives the best accuracy because it considers points on both sides of \( \large x \).

 

 

Example

Suppose we want to calculate the derivative of \( \large f(x) = x^2 \) at the point \( \large x = 1 \) with \( \large h = 0{,}1 \).

 

The necessary function values are:

 

$$ \large f(1+h) = f(1{,}1) = 1{,}21, \quad f(1-h) = f(0{,}9) = 0{,}81 $$

 

Substituting into the formulas:

 

$$ \large f'_{\text{forward}}(1) = \frac{1{,}21 - 1}{0{,}1} = 2{,}1 $$

$$ \large f'_{\text{backward}}(1) = \frac{1 - 0{,}81}{0{,}1} = 1{,}9 $$

$$ \large f'_{\text{central}}(1) = \frac{1{,}21 - 0{,}81}{0{,}2} = 2{,}0 $$

 

The true value of \( \large f'(x) = 2x \) is \( \large 2 \), so the central difference gives the most accurate result.

 

 

 

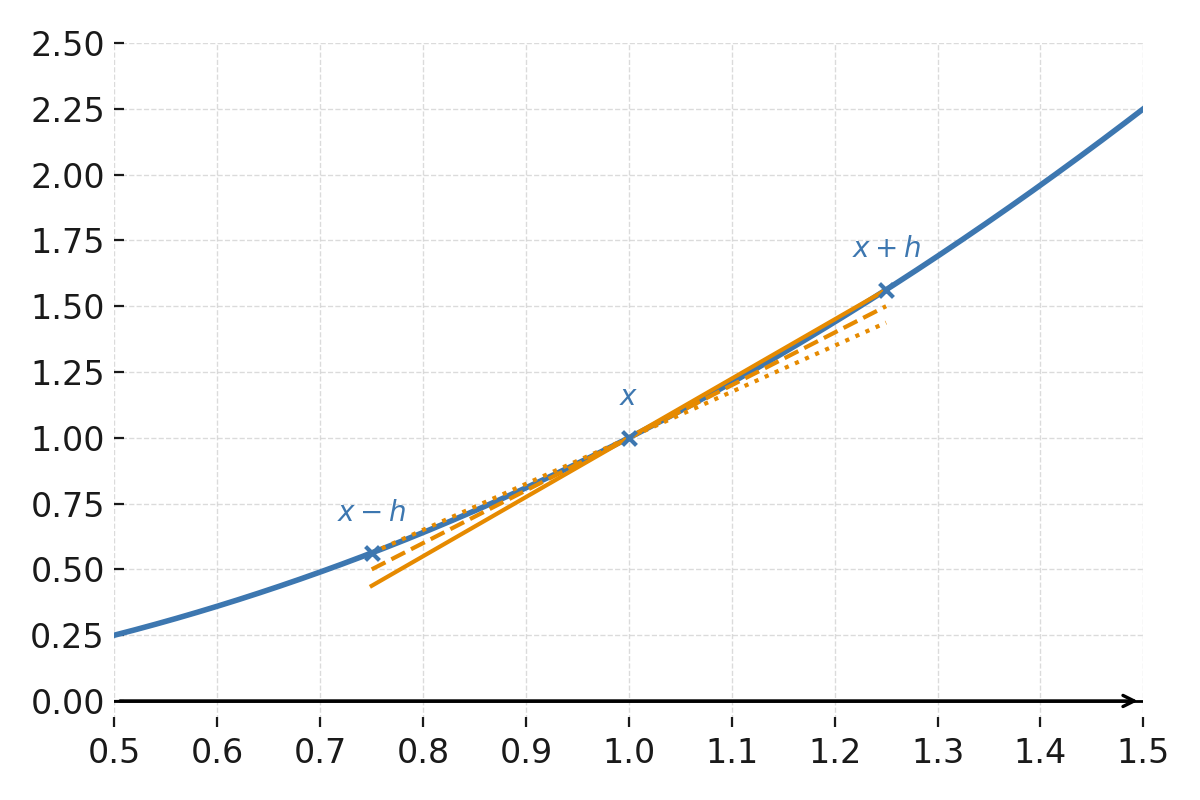
The function \( \large f(x) = x^2 \) around the point \( \large x=1 \).

The three slopes (forward, backward, and central) show the difference between using the points \( \large (x,f(x)) \), \( \large (x+h,f(x+h)) \), and \( \large (x-h,f(x-h)) \).

 

 

Remarks

The accuracy depends on how small \( \large h \) is. Too large an \( \large h \) gives a poor approximation, while too small an \( \large h \) may lead to rounding errors. In practice, \( \large h \) is chosen so that the difference quotient is stable and provides reasonable accuracy.