Volume with vectors

The volume of a solid in space can be calculated using vectors. In particular, parallelepipeds (boxes) can be expressed in a simple formula when they are described by three vectors.

 

Volume of a parallelepiped

For three vectors \( \large \mathbf{u}, \mathbf{v}, \mathbf{w} \) in space, the volume of the parallelepiped spanned by them is given by:

 

$$ \large V = \left| \det \begin{pmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{pmatrix} \right| $$

 

where \( \large \mathbf{u} = (x_1,y_1,z_1) \), \( \large \mathbf{v} = (x_2,y_2,z_2) \), and \( \large \mathbf{w} = (x_3,y_3,z_3) \).

 

 

Example

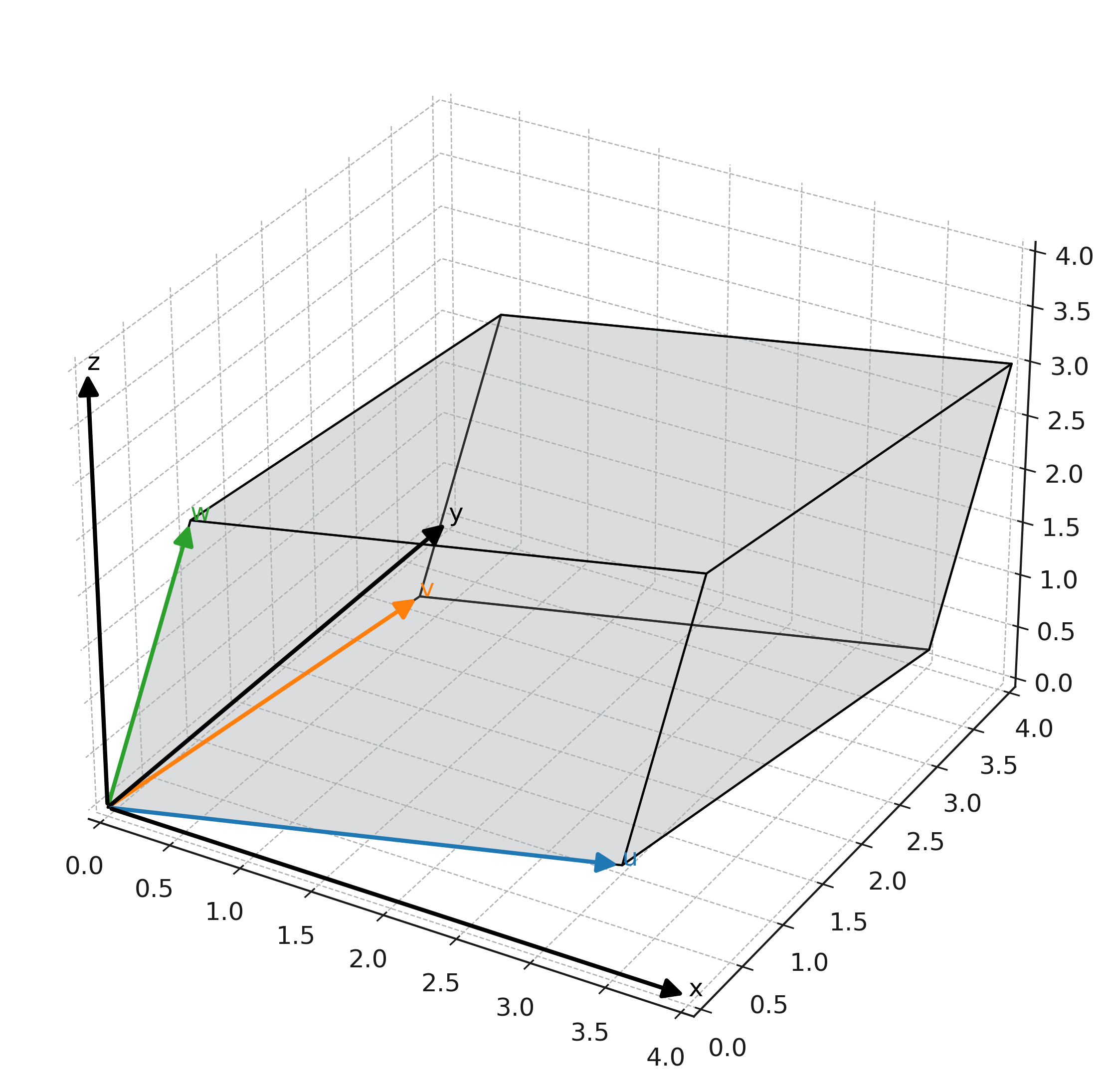
We take \( \large \mathbf{u} = (3,1,0) \), \( \large \mathbf{v} = (1,2,1) \), and \( \large \mathbf{w} = (0,1,2) \).

 

$$ \large V = \left| \det \begin{pmatrix} 3 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 2 \end{pmatrix} \right| $$

 

When calculating a determinant, you can expand it along any row or column. The result will always be the same, regardless of which you choose. For simplicity, we expand here along the first row.

 

$$ \large V= 3 \cdot \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} + 0 \cdot \det \begin{pmatrix} 1 & 2 \\ 0 & 1 \end{pmatrix} $$

 

The small determinants are calculated separately:

$$ \large \det \begin{pmatrix} 2 & 1 \\ 1 & 2 \end{pmatrix} = 2 \cdot 2 - 1 \cdot 1 = 3 $$

$$ \large \det \begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix} = 1 \cdot 2 - 1 \cdot 0 = 2 $$

 

We now substitute the results back into the expression:

 

$$ \large V = | 3 \cdot 3 - 1 \cdot 2 + 0 | = | 9 - 2 | = | 7 | = 7 $$

 

The volume of the parallelepiped is therefore 7. We use the absolute value because a determinant can be negative depending on the orientation of the vectors, but volume can never be less than zero.

 

 

Geometric interpretation

The formula corresponds to calculating base area times height. The base area is found using an area calculation, and the height is obtained by projecting the third vector perpendicularly onto the base.

 

Application

Volume formulas with vectors are used in geometry, linear algebra, and physics. They make it possible to calculate the volume of boxes and other solids in coordinate systems, and form the basis for further topics such as determinants, the cross product, and integrals.