Cross product

The cross product of two vectors in space is a vector that is perpendicular to both of the original vectors. The cross product is used to find areas, normal vectors, and orientations in 3D geometry.

Definition

For two vectors $ \large \mathbf{u} = (x_1,y_1,z_1) $ and $ \large \mathbf{v} = (x_2,y_2,z_2) $, the cross product is defined by the determinant:

$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \end{vmatrix} = (y_1z_2 - z_1y_2,\; z_1x_2 - x_1z_2,\; x_1y_2 - y_1x_2) $$

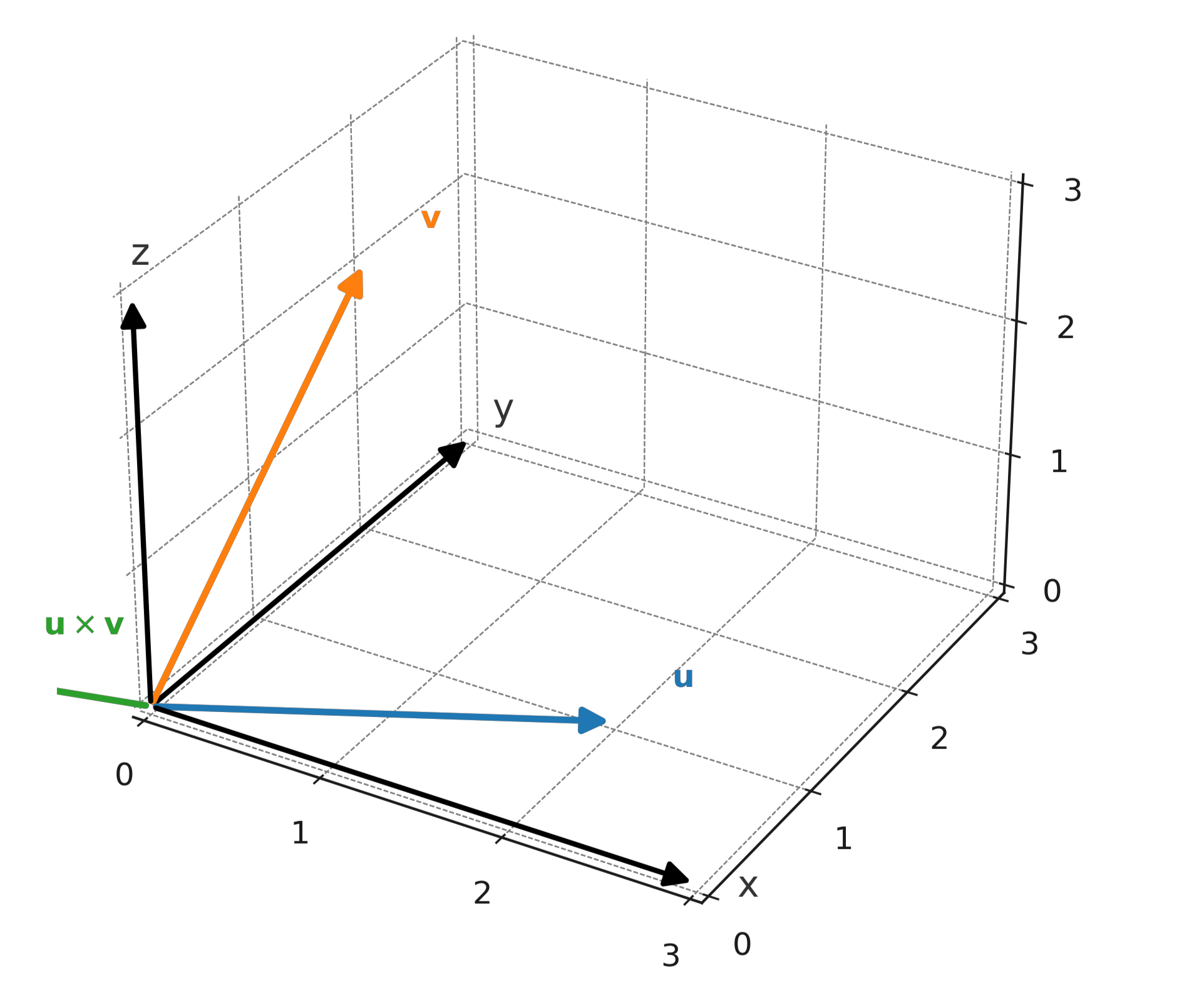
Example

We take $ \large \mathbf{u} = (1,2,3) $ and $ \large \mathbf{v} = (4,5,6) $.

$$ \large \mathbf{u} \times \mathbf{v} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = (-3,6,-3) $$

The result is a new vector $ \large (-3,6,-3) $, which is perpendicular to both $ \large \mathbf{u} $ and $ \large \mathbf{v} $.

Geometric interpretation

The length of the cross product corresponds to the area of the parallelogram spanned by the vectors:

$$ \large |\mathbf{u} \times \mathbf{v}| = |\mathbf{u}| \cdot |\mathbf{v}| \cdot \sin(\theta) $$

The direction is determined by the right-hand rule: If you point the index finger of your right hand in the direction of $ \large \mathbf{u} $ and the middle finger in the direction of $ \large \mathbf{v} $, then the thumb points in the direction of $ \large \mathbf{u} \times \mathbf{v} $.

Cross product of two vectors in 3D

Application

The cross product is used in many areas of mathematics and physics:

To find a normal vector to a plane
To calculate the area of parallelograms and triangles in 3D
In mechanics to determine the moment of a force
In computer graphics to calculate the orientation of surfaces