Lines and planes in space

In space, lines and planes can be described using vectors. This makes it possible to work systematically with geometry in three dimensions.

 

Lines

A line in space can be described by a point \( \large \mathbf{a} \) and a direction vector \( \large \mathbf{r} \). All points \( \large \mathbf{x} \) on the line can be written as

 

$$ \large \mathbf{x} = \mathbf{a} + t \cdot \mathbf{r}, \quad t \in \mathbb{R} $$

 

Here, \( \large t \) is a parameter that determines how far one moves along the line.

 

Example

A line through the point \( \large (1,2,0) \) with direction vector \( \large (2,-1,3) \) is given by:

 

$$ \large \mathbf{x} = (1,2,0) + t \cdot (2,-1,3) $$

 

Planes

A plane can be described by a point \( \large \mathbf{a} \) and a normal vector \( \large \mathbf{n} \). All points \( \large \mathbf{x} \) in the plane satisfy

 

$$ \large (\mathbf{x} - \mathbf{a}) \cdot \mathbf{n} = 0 $$

 

This means that the difference between any point in the plane and the point \( \large \mathbf{a} \) is perpendicular to the normal vector.

 

Example

A plane through the point \( \large (1,0,2) \) with normal vector \( \large (2,-1,1) \) can be described as

 

$$ \large 2(x-1) -1(y-0) + 1(z-2) = 0 $$

 

or rewritten as:

 

$$ \large 2x - y + z = 4 $$

 

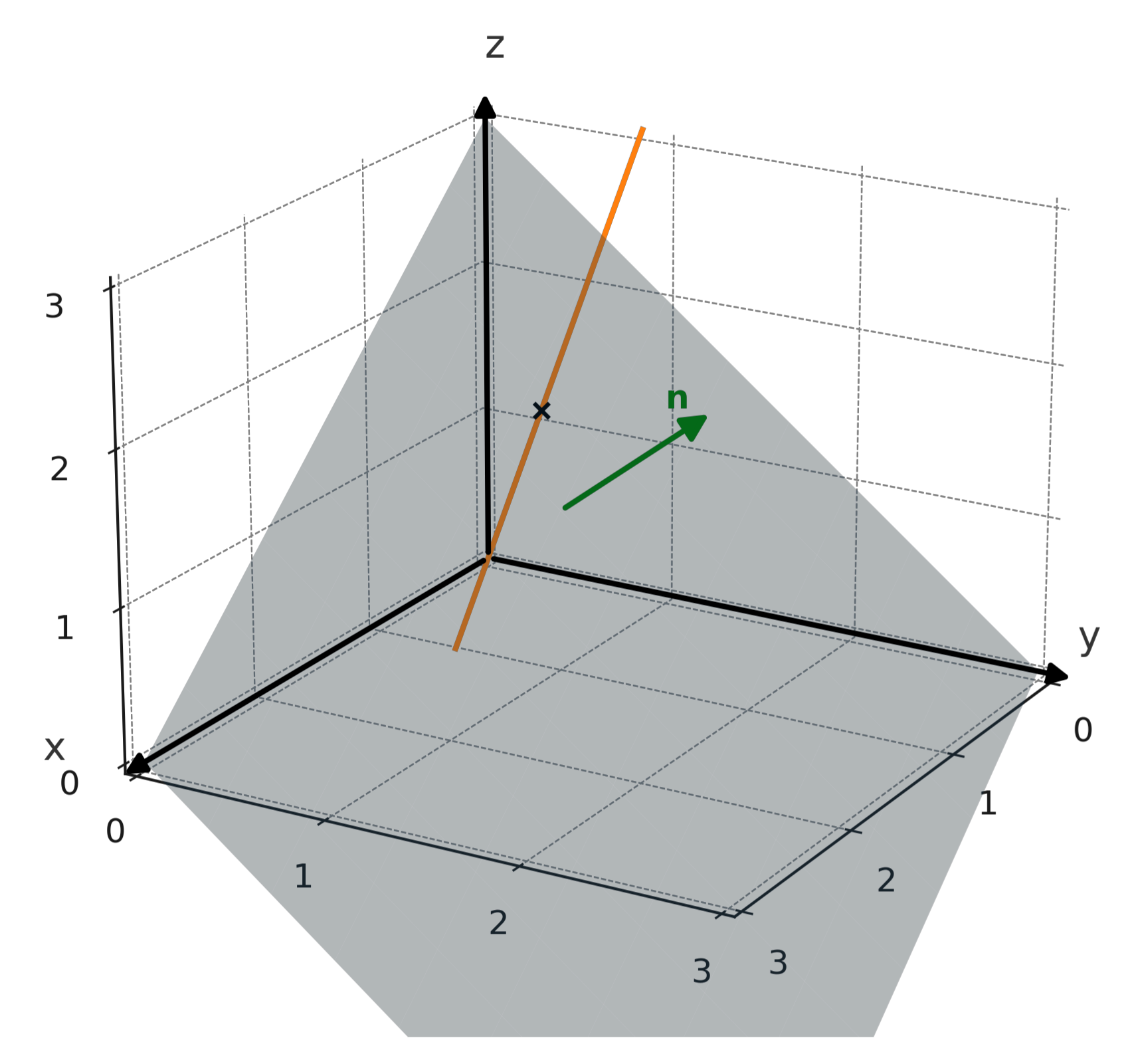
Geometric interpretation

A line describes all points along a direction, while a plane describes all points in an infinite "flat layer". The normal vector (n) to a plane points perpendicular to this surface.

 

The intersection between a line and a plane can be a single point, marked with a cross in the illustration below.

It can also be the entire line, if the line lies in the plane, or it can be empty, if the line is parallel to and outside the plane.

 

 

Application

Lines and planes in space are central in geometry, physics, and computer science. They are used, for example, to describe trajectories, reflections, 3D modeling, and collision detection in computer graphics.