Coordinates in 3D

In 3D space, a point is described by three coordinates. Whereas in the plane we use two numbers to specify a position, in space three numbers are required to determine a point uniquely.

 

Definition

A point \( \large P \) in space is given as

 

$$ \large P = (x,y,z) $$

 

Here \( \large x \) is the distance along the x-axis, \( \large y \) the distance along the y-axis, and \( \large z \) the distance along the z-axis.

 

 

Example

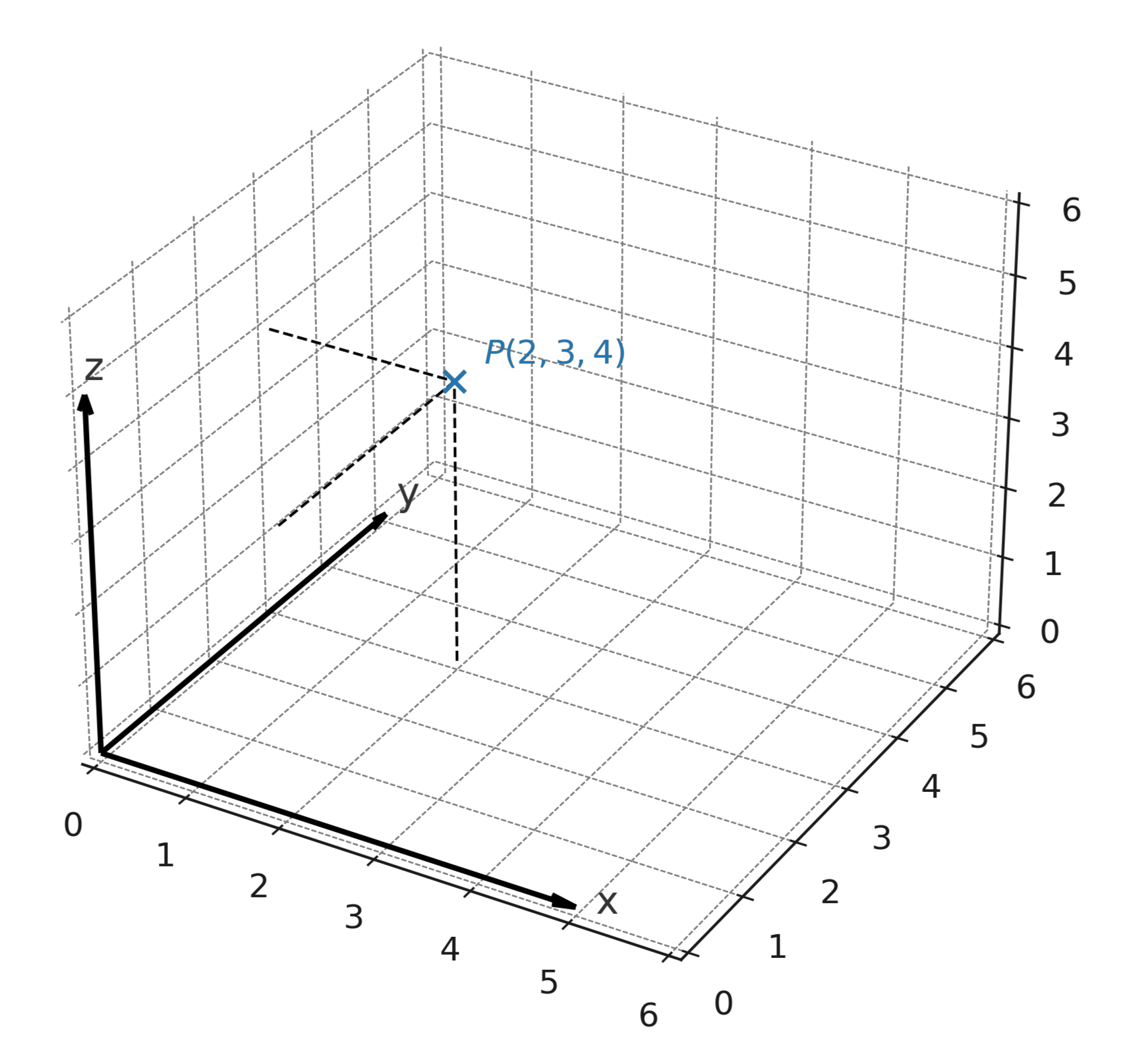
The point \( \large P = (2,3,4) \) means moving 2 units along the x-axis, 3 units along the y-axis, and 4 units up along the z-axis.

 

 

Coordinate axes and origin

The three axes are called the x-, y-, and z-axes. Their common starting point is called the origin and has the coordinates

 

$$ \large O = (0,0,0) $$

 

A vector from the origin to a point \( \large P=(x,y,z) \) is written as

 

$$ \large \vec{OP} = (x,y,z) $$

 

 

Distance in space

The distance from the origin to a point \( \large (x,y,z) \) is found by extending Pythagoras’ theorem:

 

$$ \large |(x,y,z)| = \sqrt{x^2 + y^2 + z^2} $$

 

This is the length of the vector from the origin to the point.

 

 

Geometric interpretation

A coordinate system in space is built from three mutually perpendicular axes. Each point can be seen as a corner of a rectangular prism with the origin as the starting point.

 

 

Application

Coordinates in 3D are used everywhere in mathematics, physics, and computer science, for example to describe points in geometry, positions in space, or objects in 3D graphics.