Multiplication by a scalar

When a vector is multiplied by a number, its length changes, but the direction is preserved if the number is positive. If the number is negative, the vector is reversed in the opposite direction.

 

Definition

For a vector \( \large \mathbf{v} = (x,y) \) and a number \( \large k \), we have:

 

$$ \large k \cdot (x,y) = (k \cdot x,\; k \cdot y) $$

 

Examples

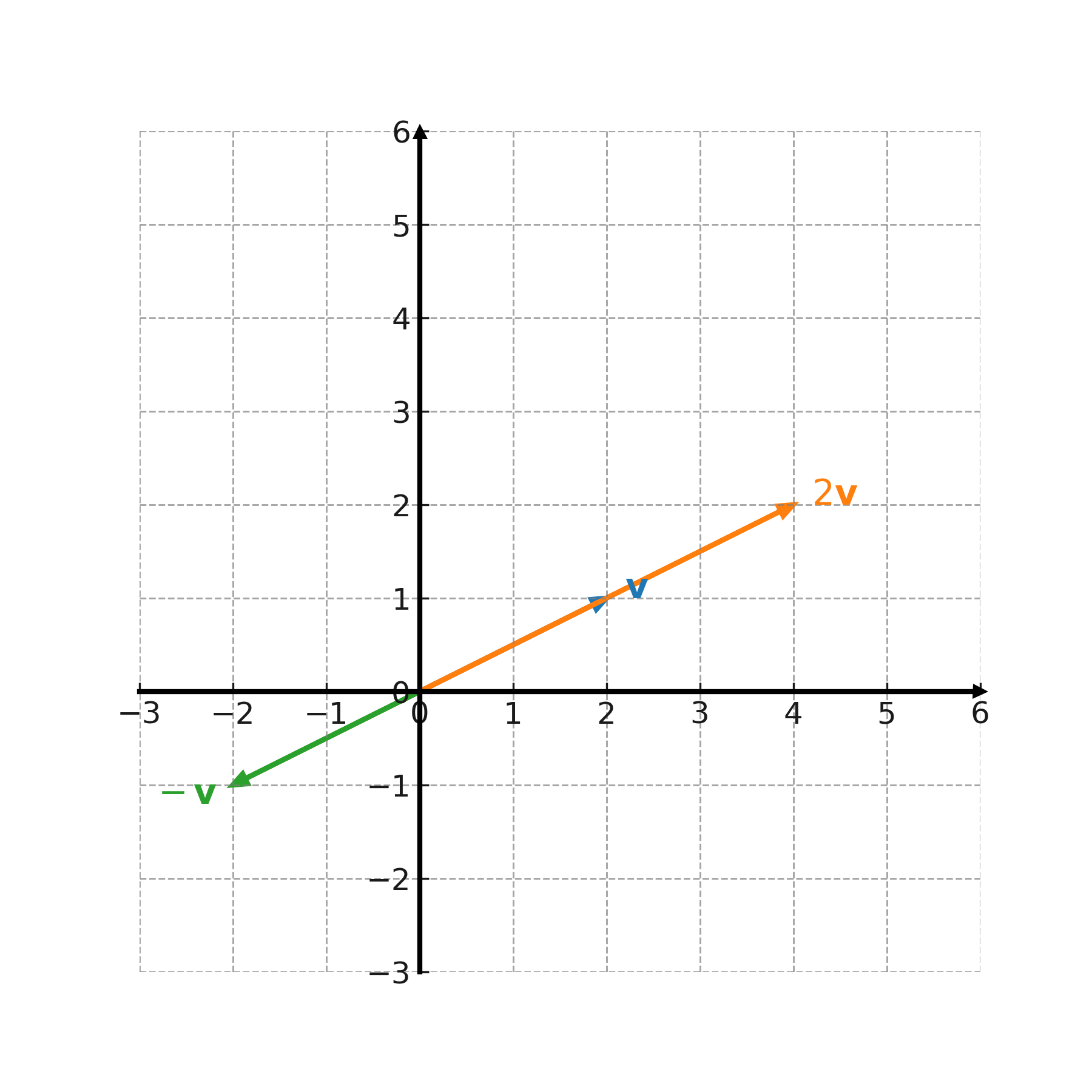
We consider the vector \( \large \mathbf{v} = (2,1) \).

 

When \( \large k = 2 \):

$$ \large 2 \cdot (2,1) = (4,2) $$

 

When \( \large k = -1 \):

$$ \large -1 \cdot (2,1) = (-2,-1) $$

 

When \( \large k = \frac{1}{2} \):

$$ \large \frac{1}{2} \cdot (2,1) = (1,\; \frac{1}{2}) $$

 

When \( \large k = 0 \):

$$ \large 0 \cdot (2,1) = (0,0) $$

 

Geometric interpretation

Multiplication by a number stretches or shrinks the vector. For positive numbers, the direction is preserved, for negative numbers, the direction is reversed. When the number is between 0 and 1, the vector becomes shorter, and when the number is 0, we obtain the zero vector.

 

 

Application

Multiplication by numbers is used to change the magnitude of a movement or a force. In physics, this corresponds to changing the strength of a force without changing its direction.

 

In mathematics, multiplication by parameters is used to describe lines and curves, for example \( \large (x,y) = (x_0,y_0) + t \cdot \mathbf{r} \), where \( \large t \) is a number and \( \large \mathbf{r} \) a direction vector.