Addition and subtraction

When working with vectors in the plane, you can add or subtract them. This is done by combining the coordinates of each vector.

 

Definition

For two vectors \( \large \mathbf{u} = (x_1,y_1) \) and \( \large \mathbf{v} = (x_2,y_2) \), we have:

 

$$ \large \mathbf{u} + \mathbf{v} = (x_1 + x_2,\; y_1 + y_2) $$

 

$$ \large \mathbf{u} - \mathbf{v} = (x_1 - x_2,\; y_1 - y_2) $$

 

 

Example

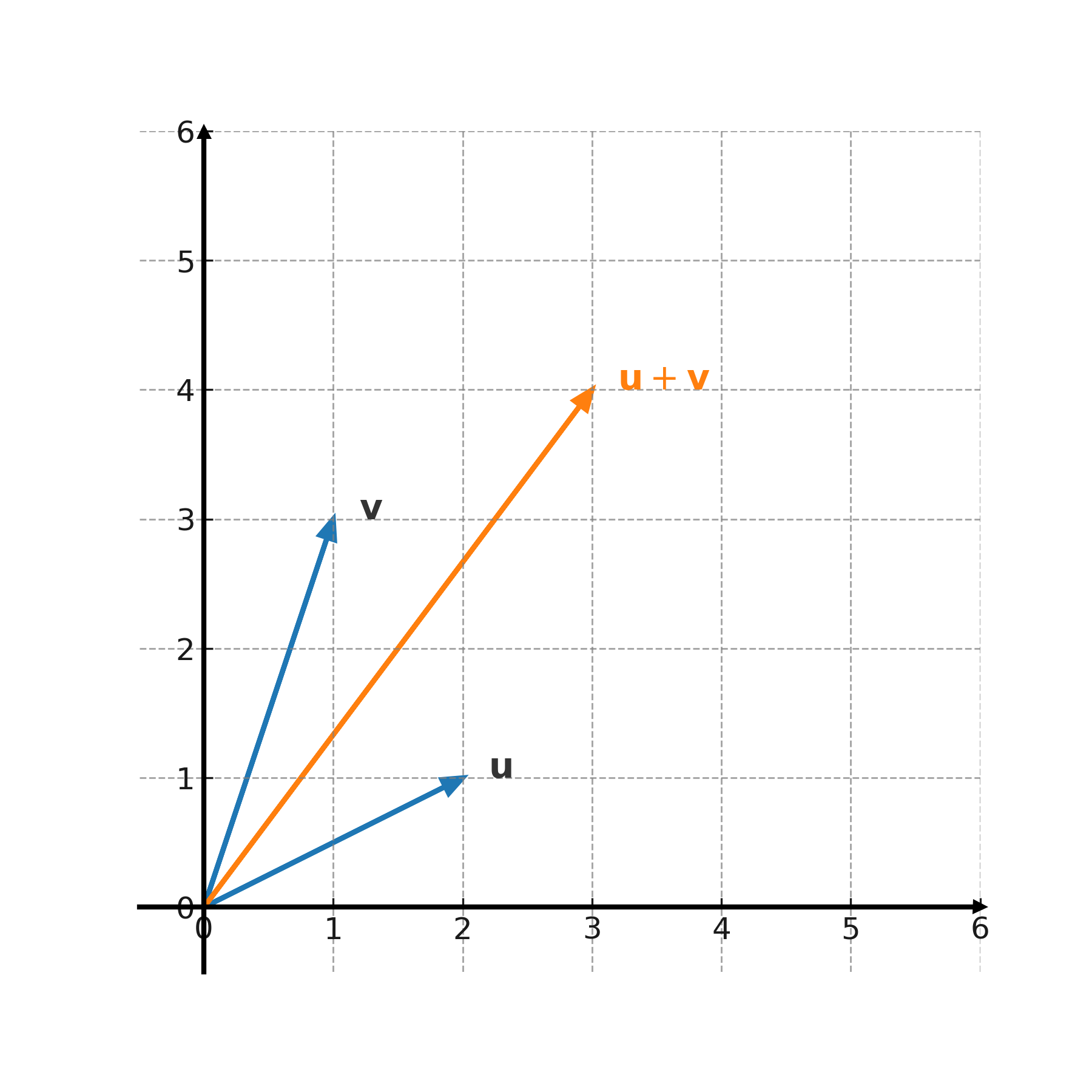
We want to calculate the sum and the difference of the vectors \( \large \mathbf{u} = (2,1) \) and \( \large \mathbf{v} = (1,3) \).

 

The sum is:

 

$$ \large (2,1) + (1,3) = (2+1,\; 1+3) = (3,4) $$

 

 

The difference is:

 

$$ \large (2,1) - (1,3) = (2-1,\; 1-3) = (1,-2) $$

 

 

Geometric interpretation

The addition can be shown graphically with the parallelogram method: place the vectors tail to tail and draw two copies so that a parallelogram is formed. The diagonal represents the sum.

 

 

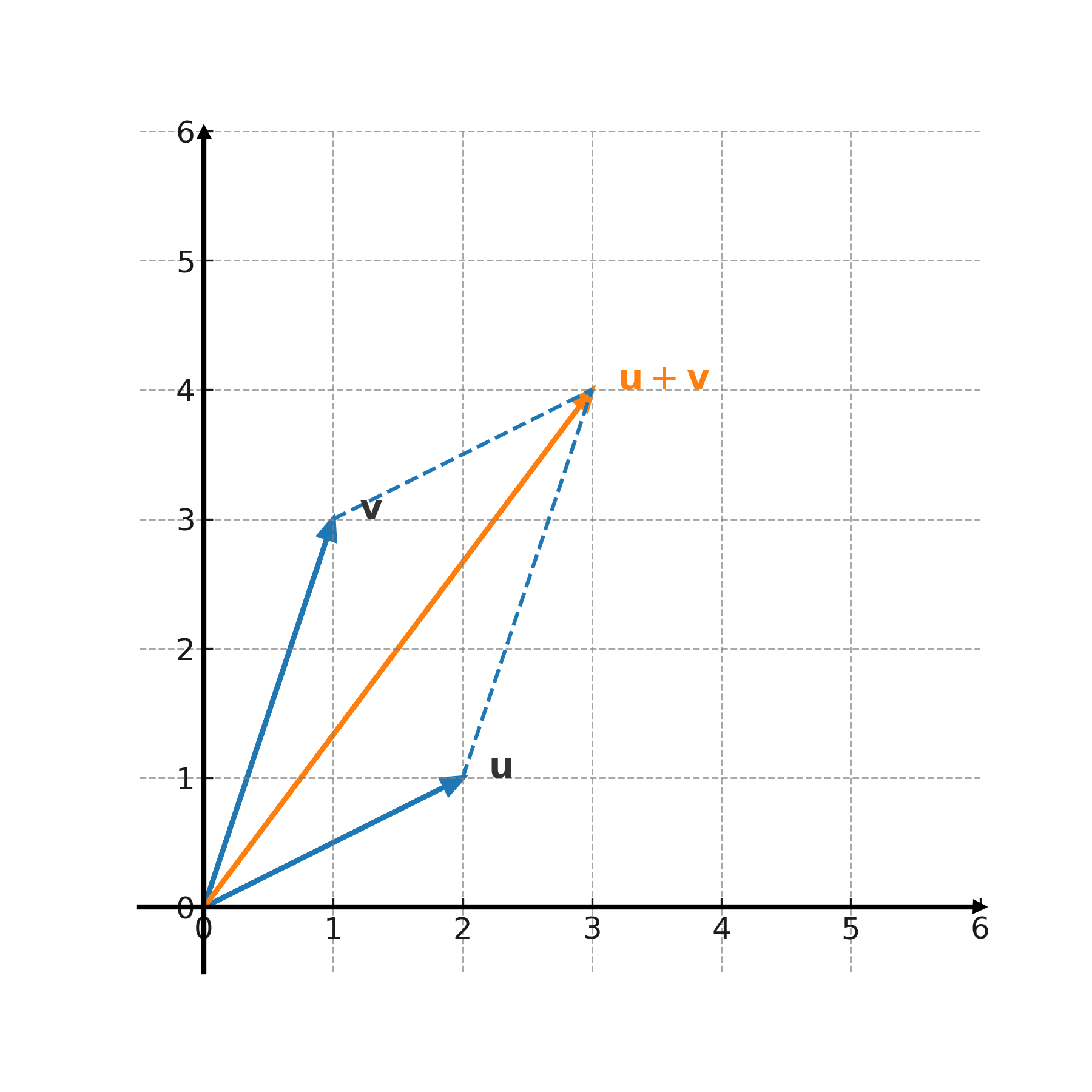
The subtraction can be seen as the addition of the opposite vector. For example, \( \large \mathbf{u} - \mathbf{v} = \mathbf{u} + (-\mathbf{v}) \).

 

 

Application

In physics, vector addition is used to determine the total force on a body. If a box is pulled in one direction by one force and in another direction by another force, the resulting motion is given by the sum of the two force vectors.