Length and unit vectors

The length of a vector describes how large the vector is, while a unit vector is a vector with length 1 in the same direction as the original.

 

Length

For a vector \( \large \mathbf{v} = (x,y) \), the length is found by:

 

$$ \large |\mathbf{v}| = \sqrt{x^2 + y^2} $$

 

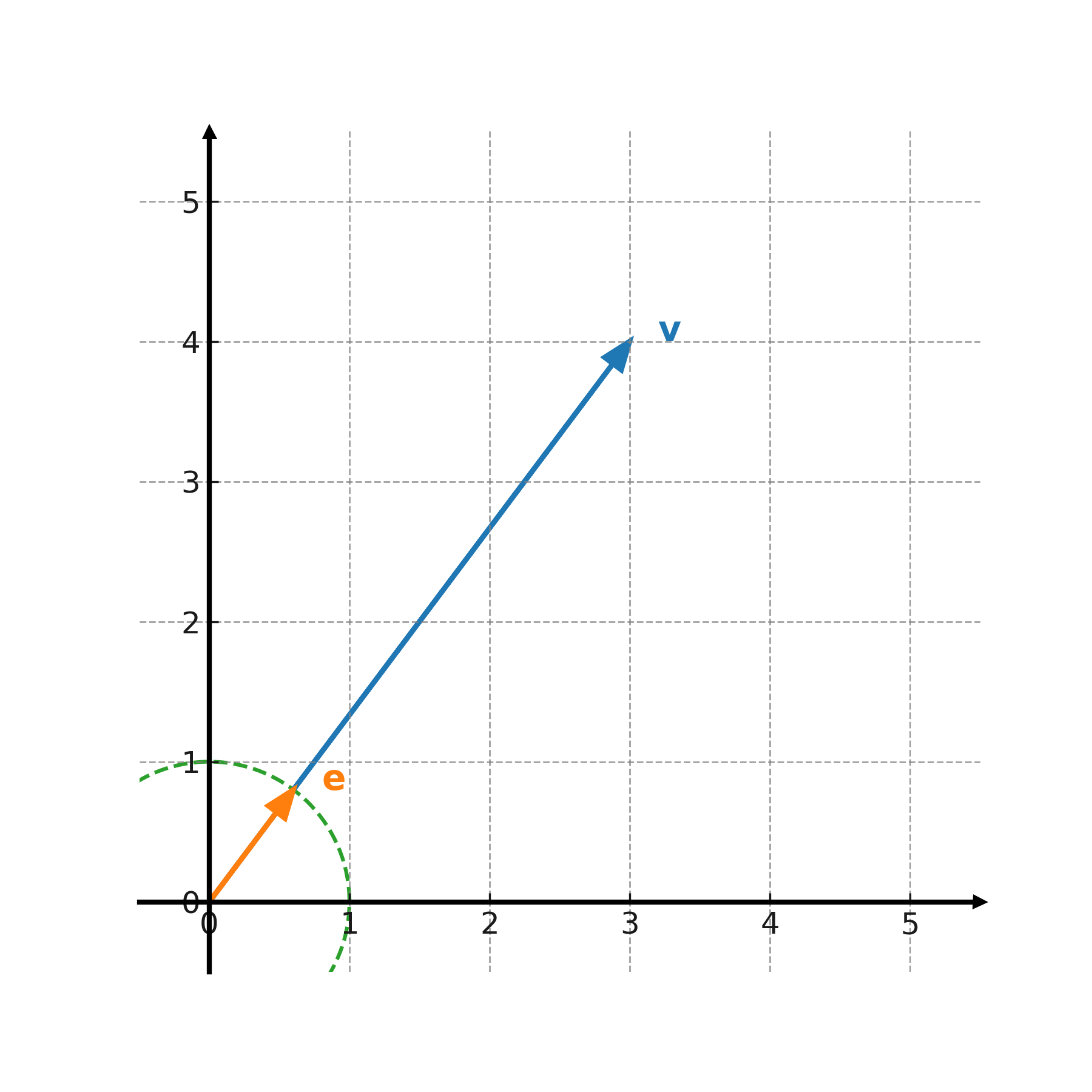
Example: The vector \( \large \mathbf{v} = (3,4) \) has the length

 

$$ \large |\mathbf{v}| = \sqrt{3^2 + 4^2} = 5 $$

 

Unit vector

A unit vector is found by dividing a vector by its length:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Example: For \( \large \mathbf{v} = (3,4) \) we get

 

$$ \large \mathbf{e} = \frac{1}{5} \cdot (3,4) = \left(\frac{3}{5}, \frac{4}{5}\right) $$

 

Note: The zero vector \( \large (0,0) \) cannot be turned into a unit vector because its length is 0, and you cannot divide by 0.

 

The best-known unit vectors are the standard unit vectors in the coordinate system:

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Geometric interpretation

The length of a vector corresponds to the distance from the origin to the vector’s endpoint.

A unit vector is an arrow in the same direction, but always with length 1.

 

 

Application

Unit vectors are used to describe directions, without the magnitude mattering. In physics, they are used for example to indicate the direction of a force independently of its strength, and in mathematics they are used to define the axes of coordinate systems.