A triangular prism is a three-dimensional geometric figure that has two parallel and congruent triangular bases. The three remaining faces are rectangles or parallelograms.

A triangular prism is therefore a special case of a prism where the base is a triangle.

 

 

 

Volume

The volume of a triangular prism is found by multiplying the area of the base by the prism’s height (the distance between the two triangular faces):

 

$$ \large V = A_{base} \cdot h $$

 

If the base is a triangle with base \( \large g \) and height \( \large h_t \), then the area is:

 

$$ \large A_{base} = \frac{1}{2} g \cdot h_t $$

 

The volume is therefore:

 

$$ \large V = \frac{1}{2} g \cdot h_t \cdot h $$

 

If the prism is oblique, then the height is not the slanted side length, but the perpendicular distance between the two triangular faces. If the slanted side is \( \large s \), and the angle to the base is \( \large \theta \), the real height is:

 

$$ \large h = s \cdot \sin(\theta) $$

 

Example

We will calculate the volume of a triangular prism where the base is a right-angled triangle with base \( \large g = 6 \,\text{cm} \), triangle height \( \large h_t = 4 \,\text{cm} \), and the prism has a height (depth) of \( \large h = 10 \,\text{cm} \).

 

First, find the area of the base:

 

$$ \large A_{base} = \tfrac{1}{2} \cdot 6 \cdot 4 = 12 \,\text{cm}^2 $$

 

Then, find the volume:

 

$$ \large V = 12 \cdot 10 = 120 \,\text{cm}^3 $$

 

 

Example of an oblique triangular prism

 

 

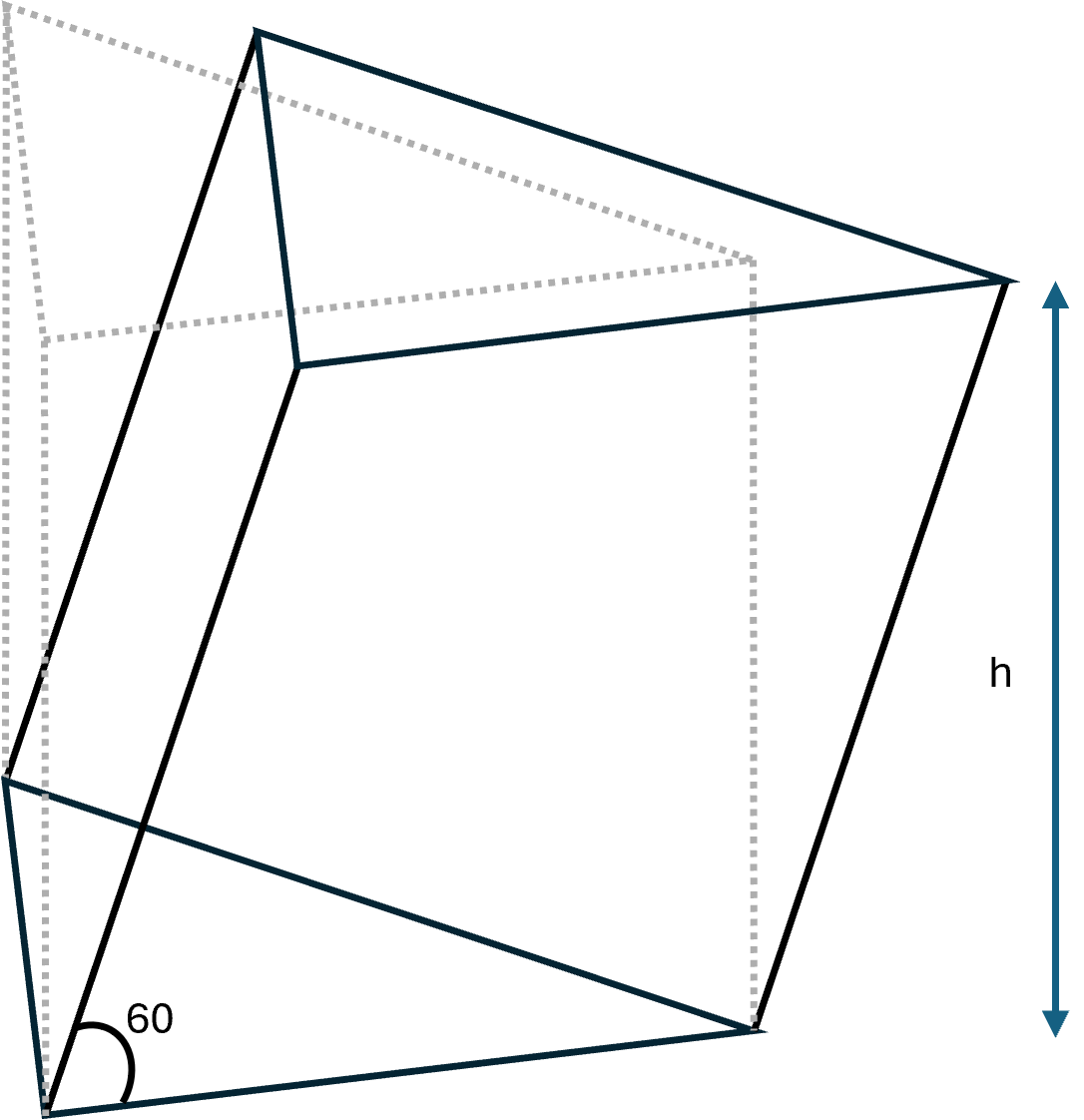
Suppose we have a triangular prism where the base is a triangle with base \( \large g = 5 \,\text{cm} \) and triangle height \( \large h_t = 3 \,\text{cm} \). The base area is therefore:

 

$$ \large A_{base} = \tfrac{1}{2} \cdot 5 \cdot 3 = 7.5 \,\text{cm}^2 $$

 

The slanted side of the prism is \( \large s = 12 \,\text{cm} \), and the angle to the base is \( \large 60^\circ \). The real height is:

 

$$ \large h = s \cdot \sin(60^\circ) = 12 \cdot \tfrac{\sqrt{3}}{2} \approx 10.39 \,\text{cm} $$

 

The volume is therefore:

 

$$ \large V = A_{base} \cdot h = 7.5 \cdot 10.39 \approx 77.9 \,\text{cm}^3 $$

 

 

Surface area

The surface area of a triangular prism consists of two congruent triangular faces and three rectangular faces. The area therefore depends on the sides of the triangle and the prism’s height.

In general, the formula is:

 

$$ \large O = 2 \cdot A_{base} + (a + b + c) \cdot h $$

 

where \( \large a, b, c \) are the side lengths of the triangle, and \( \large h \) is the height of the prism.