The normal distribution is one of the most important probability distributions in statistics. It is used to describe many phenomena in nature and society where data is distributed around an average. Examples include heights, measurement errors, and grade averages.

 

Definition

A random variable \(\large X\) is said to be normally distributed with mean \(\large \mu\) and variance \(\large \sigma^2\) if it has the density function:

 

$$ \large f(x) = \frac{1}{\sigma \sqrt{2\pi}} \, e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty $$

 

Here \(\large \mu\) is the center of the distribution (the mean), and \(\large \sigma\) determines how spread out the values are around this center.

 

Properties

 

• Mean: \( \mu \)
• Variance: \( \sigma^2 \)
• Standard deviation: \( \sigma \)
• Symmetric around the mean
• Bell-shaped curve that never touches the x-axis

 

 

Standard normal distribution

If we set \( \large \mu = 0 \) and \( \large \sigma = 1 \), we obtain the standard normal distribution:

 

$$ \large Z \sim N(0,1) $$

 

Any normally distributed variable can be transformed into a standard normal via the transformation:

 

$$ \large Z = \frac{X - \mu}{\sigma} $$

 

The standard normal distribution is used because there are tables and computer functions to calculate probabilities based on \(\large Z\).

 

 

Example

Assume that the height of adult men is normally distributed with mean \(\large \mu = 180\) cm and standard deviation \(\large \sigma = 10\) cm.

 

What is the probability that a randomly chosen man is between 170 and 190 cm tall?

 

We transform to the standard normal:

 

$$ \large Z_1 = \frac{170 - 180}{10} = -1 $$

$$ \large Z_2 = \frac{190 - 180}{10} = 1 $$

 

The probability is therefore:

 

$$ \large P(170 \leq X \leq 190) = P(-1 \leq Z \leq 1) = F(1) - F(-1) $$

 

where \(F(z)\) is the cumulative distribution function:

 

$$ \large F(z) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{z} e^{-\tfrac{t^2}{2}} \, dt $$

 

The value of the integral cannot be calculated in closed form, but it can be read from tables. For \(\large z = 1\) and \(\large z = -1\) we have:

 

$$ \large F(1) \approx 0,8413 \quad \text{and} \quad F(-1) \approx 0,1587 $$

 

Thus the probability becomes:

 

$$ \large P(-1 \leq Z \leq 1) = 0,8413 - 0,1587 = 0,6826 $$

 

So about 68% of all observations lie within one standard deviation of the mean.

 

 

68-95-99.7 rule

An important rule of thumb for the normal distribution is that probabilities are distributed in a certain way around the mean:

 

• About 68% of all observations lie within 1 standard deviation (\(\large \mu \pm 1\sigma\))
• About 95% lie within 2 standard deviations (\(\large \mu \pm 2\sigma\))
• About 99.7% lie within 3 standard deviations (\(\large \mu \pm 3\sigma\))

 

The rule shows that most observations lie close to the mean, while extreme values are very rare.

 

 

Graph

The curve of the normal distribution has the familiar bell shape and shows the distribution with the mean in the center and decreasing probability to both sides.

 

 

 

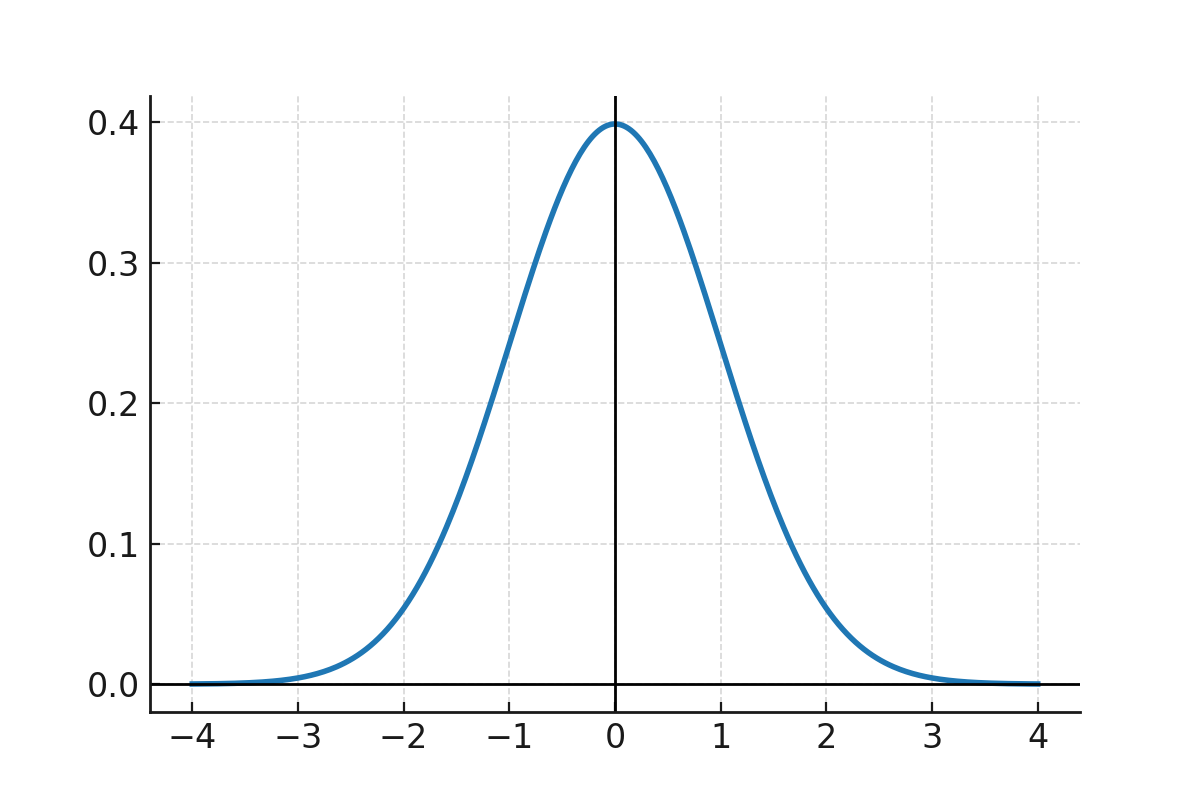
The curve shows the density function. The height of the curve is not a probability in itself, but probabilities are found by calculating the area under the curve over an interval.

For the standard normal distribution, the density function peaks at the mean with the value:

 

$$ \large f(0) = \frac{1}{\sqrt{2\pi}} \approx 0,3989 $$

 

This means that the graph reaches about 0.4 on the y-axis. This is consistent with the definition and is not a probability in itself.

For example, the probability of lying within one standard deviation of the mean is about 68%, even though the height of the curve at \(\large \mu\) is about 0.4.

 

 

Relation to the binomial distribution

When the number of trials \(\large n\) in a binomial distribution is large, and the probability \(\large p\) is not too close to 0 or 1, the binomial distribution can be approximated by a normal distribution:

 

$$ \large X \sim N(n \cdot p,\; n \cdot p \cdot (1-p)) $$

 

Here one often uses a so-called continuity correction, where the limits are adjusted by 0.5 to account for the fact that the binomial distribution is discrete and the normal distribution is continuous.