Binomial distribution
The binomial distribution is a probability distribution that describes the likelihood of obtaining a certain number of successes in a series of independent trials.
Each trial has only two possible outcomes: success or failure. Examples include heads or tails, hit or miss, pass or fail.
Assumptions
- A fixed number of trials, \( \large n \).
- Each trial has two outcomes: success or failure.
- The probability of success is the same in each trial, \( \large p \).
- The trials are independent of each other.
The formula
The probability of obtaining exactly \( \large r \) successes in \( \large n \) trials is:
$$ \large P(X=r) = \binom{n}{r} p^r (1-p)^{n-r} $$
Here \(\large \binom{n}{r}\) is a combination, indicating how many ways the \( \large r \) successes can be placed among the \( \large n \) trials.
Example 1: Coin toss
A coin is tossed 10 times. The probability of heads is \( \large p = 0.5 \).
What is the probability of obtaining exactly 6 heads?
$$ \large P(X=6) = \binom{10}{6} (0.5)^6 (0.5)^{4} $$
$$ \large P(X=6) = 210 \cdot (0.5)^{10} $$
$$ \large P(X=6) \approx 0.205 $$
Thus, there is about a 20.5% probability of obtaining 6 heads.
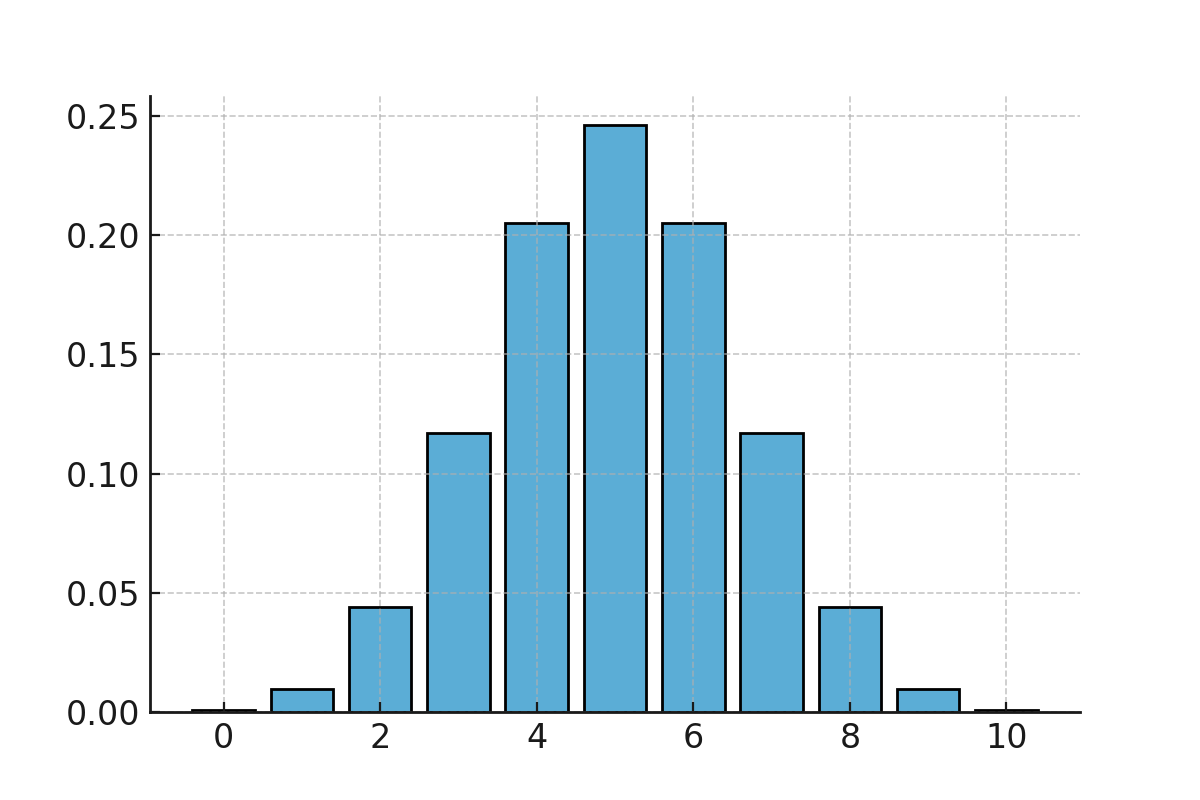
The binomial distribution for coin tosses
Example 2: Dice
A die is rolled 5 times. We define success as rolling a six. Here \( \large p = \tfrac{1}{6} \).
The probability of obtaining exactly 2 sixes is:
$$ \large P(X=2) = \binom{5}{2} \left(\tfrac{1}{6}\right)^2 \left(\tfrac{5}{6}\right)^3 $$
$$ \large P(X=2) = 10 \cdot \tfrac{1}{36} \cdot \tfrac{125}{216} $$
$$ \large P(X=2) = \tfrac{1250}{7776} $$
$$ \large P(X=2) \approx 0.161 $$
To get an overview, we can calculate the probabilities for all possible outcomes:
| \( \large r \) | Probability \( \large P(X=r) \) |
|---|---|
| 0 | \( \large 0.401 \) |
| 1 | \( \large 0.402 \) |
| 2 | \( \large 0.161 \) |
| 3 | \( \large 0.032 \) |
| 4 | \( \large 0.003 \) |
| 5 | \( \large 0.00013 \) |
We see that it is most likely to obtain 0 or 1 six in 5 rolls, and that the probability quickly becomes very small for higher numbers.
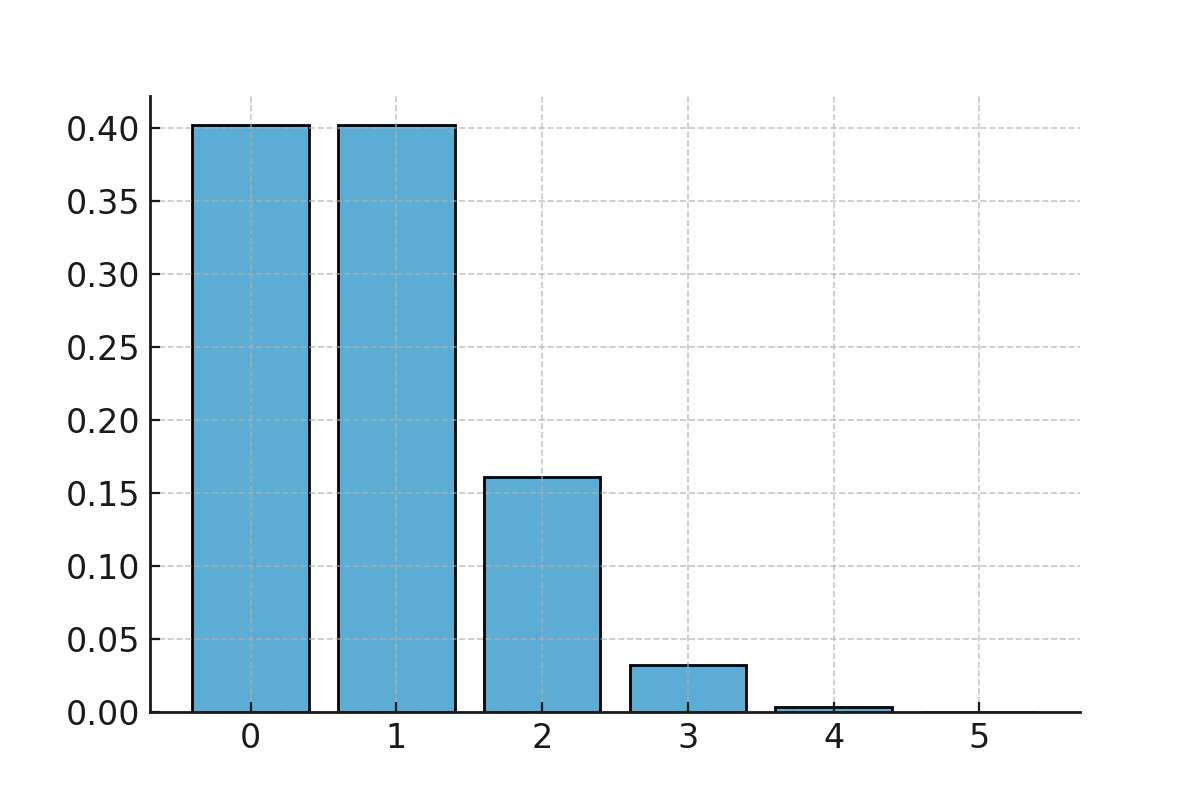
The binomial distribution for dice rolls
Example 3: Quality control
At a factory, 5% of products are defective. We randomly select 20 products. The probability of finding exactly 3 defective ones is:
$$ \large P(X=3) = \binom{20}{3} (0.05)^3 (0.95)^{17} $$
$$ \large P(X=3) = 1140 \cdot (0.000125) \cdot (0.419) $$
$$ \large P(X=3) \approx 0.059 $$
To get an overview, we can calculate the probabilities for 0 to 5 defective products:
| \( \large r \) | Probability \( \large P(X=r) \) |
|---|---|
| 0 | \( \large 0.358 \) |
| 1 | \( \large 0.377 \) |
| 2 | \( \large 0.188 \) |
| 3 | \( \large 0.059 \) |
| 4 | \( \large 0.014 \) |
| 5 | \( \large 0.003 \) |
We see that it is most likely to find 0 or 1 defective product, but there is still a real probability of finding 2 or 3 defective in a sample.
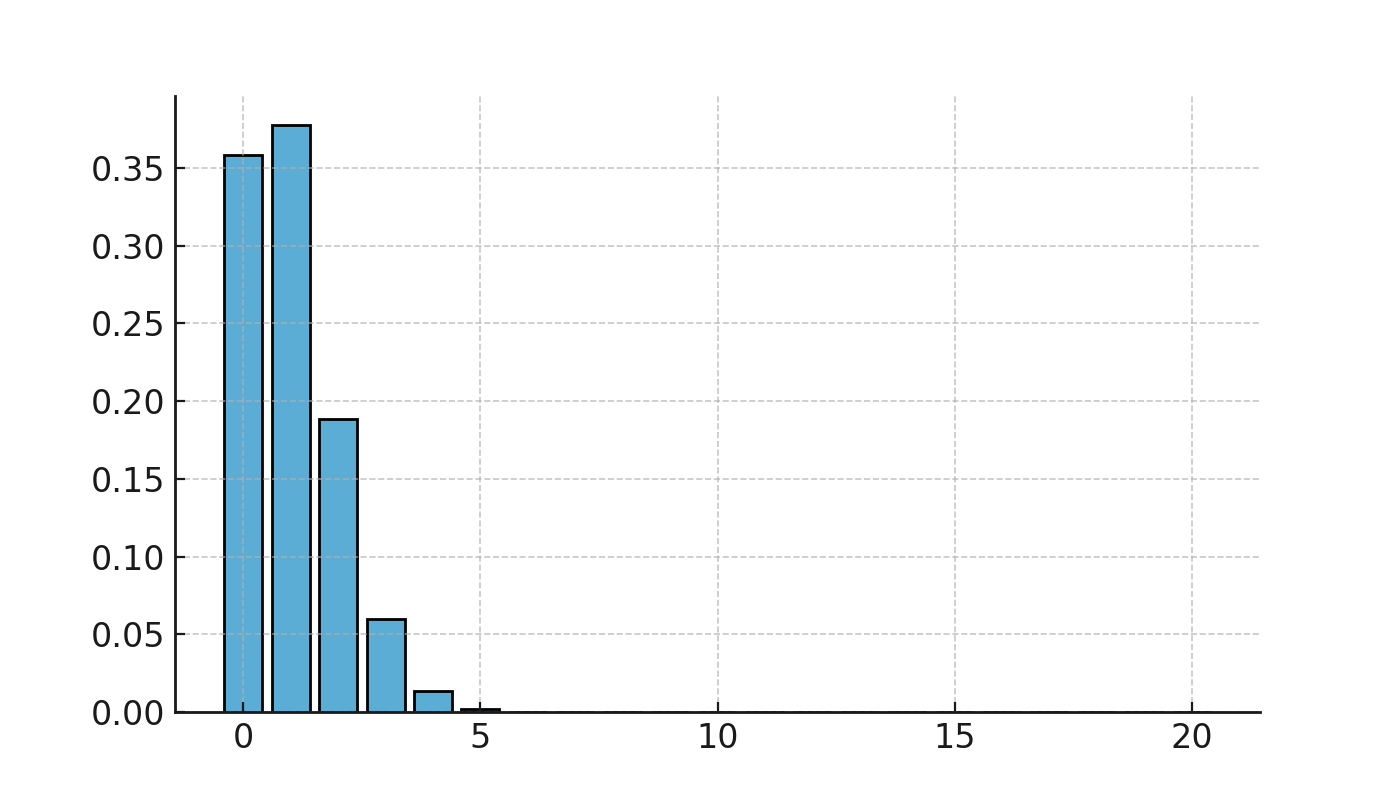
The binomial distribution in quality control
Properties
- Mean: \( \large \mu = n \cdot p \)
- Variance: \( \large \sigma^2 = n \cdot p \cdot (1-p) \)
- Standard deviation: \( \large \sigma = \sqrt{n \cdot p \cdot (1-p)} \)
Binomial and normal distribution
When \( \large n \) is large, and \( \large p \) is not too close to 0 or 1, the binomial distribution can be approximated by a normal distribution:
$$ \large N(\mu, \sigma^2) = N(n \cdot p, n \cdot p \cdot (1-p)) $$
This is useful because the normal distribution is easier to work with for large \( \large n \).
Applications
- Statistics: modeling experiments with two outcomes.
- Biology: the probability that a certain number of plants germinate.
- Medicine: the probability that a certain number of patients respond to treatment.
- Quality control: how many defective products are found in a sample.
- Games and simulations: e.g. coin tosses, dice rolls or other repeated trials.
Summary
- The binomial distribution describes the probability of a certain number of successes in \( \large n \) independent trials.
- For large \( \large n \), the binomial distribution can be approximated by a normal distribution.
- It has many applications in statistics, probability, biology, medicine, games and quality control.
The binomial distribution is one of the most fundamental distributions in probability theory and connects combinatorics with statistics.