A cone is a three-dimensional figure consisting of a circular base and a curved surface that meets at a single apex. The distance from the apex vertically down to the center of the base is called the height.

Cones can be divided into right and oblique. In a right cone, the apex lies vertically above the center of the base. 

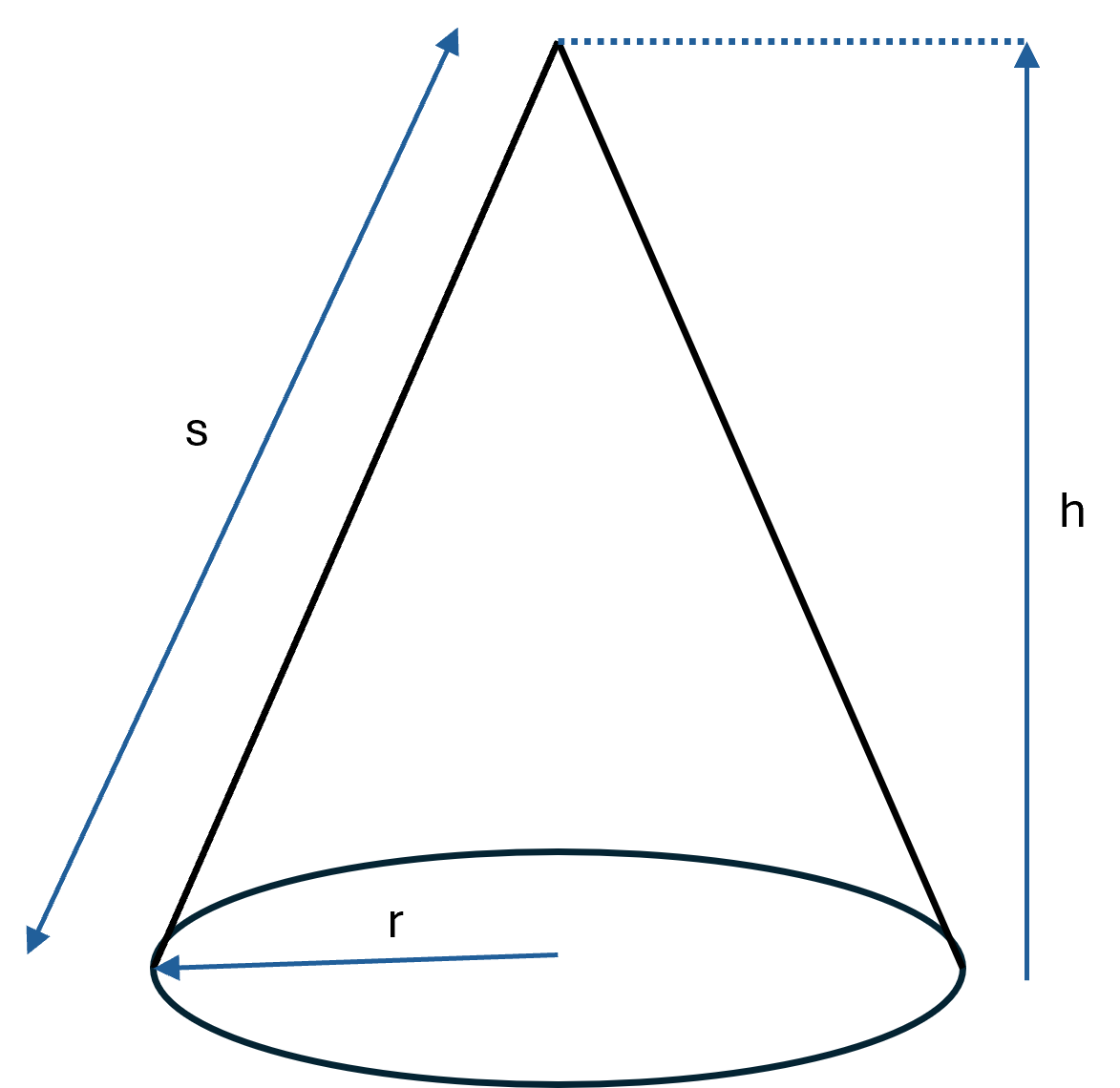
Right cone

Volume

The volume of a cone is found by multiplying the area of the base by the height and then dividing by three:

$$ \large V = \frac{1}{3} \cdot \pi \cdot r^2 \cdot h $$

Surface area

The surface area of a cone consists of the area of the base and the area of the curved surface:

$$ \large S = \pi \cdot r^2 + \pi \cdot r \cdot s $$

Here \( \large s \) is the slant height of the cone, which in a right cone can be found using Pythagoras:

$$ \large s = \sqrt{r^2 + h^2} $$

The oblique cone

In an oblique cone, the apex is shifted so that the cone leans. The volume is still calculated from the base area and the vertical height, so the volume formula is the same as for the right cone.

In an oblique cone, there is no single slant height \( \large s \). The distance from the apex to the edge of the base circle varies around the rim, so there is both a shortest and a longest distance.

Therefore, there is no simple formula for the surface area of an oblique cone. The area can, however, be determined using integral calculus or numerical methods, where the surface is described by a parameterization and the area is calculated from this.

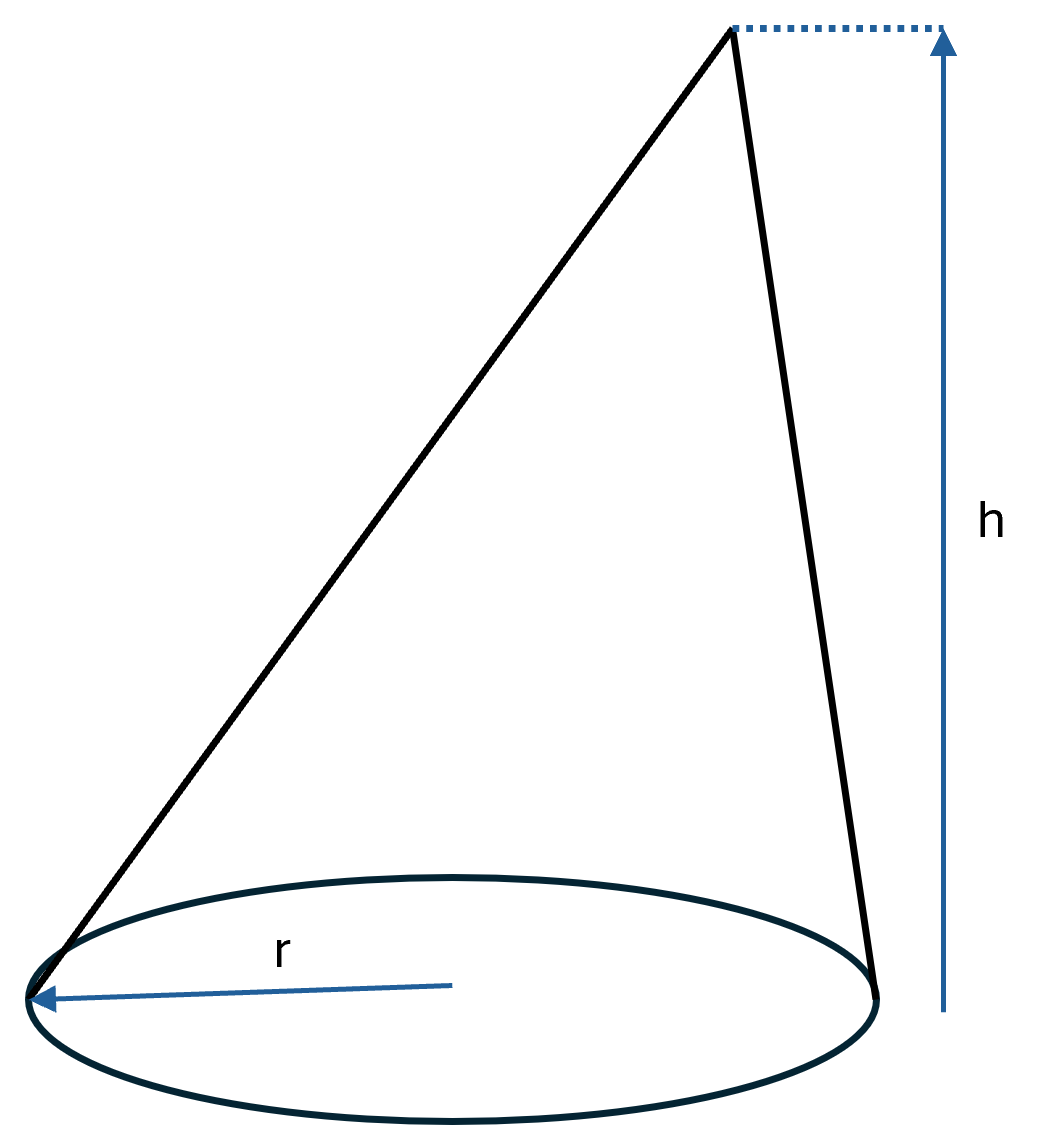
Oblique cone

Applications

Cones occur frequently in everyday life, for example in ice cream cones, traffic cones, funnels, and architectural structures.

They are also important in mathematics and physics, because volume and area can be calculated with simple formulas.