Inverse Functions

A function is bijective if it is both injective and surjective.

This means that every element in the domain \( \large A\) corresponds to exactly one element in the codomain \( \large B\), and that the entire \( \large B\) is covered.

Thus, there exists a unique correspondence that can be reversed.

 

 

Definition

A function \( \large f : A \to B\) is bijective if:

 

$$ \large \forall a_1,a_2 \in A: f(a_1)=f(a_2) \Rightarrow a_1=a_2 \quad (\text{injectivity}) $$

$$ \large \forall b \in B \;\exists a \in A : f(a)=b \quad (\text{surjectivity}) $$

 

The combination of these two properties ensures that the function can be "reversed".

 

 

Existence of an inverse function

If \( \large f : A \to B\) is bijective, there exists an inverse function \( \large f^{-1} : B \to A\), which satisfies:

 

$$ \large f^{-1}(f(a)) = a \quad \text{for all } a \in A $$

$$ \large f(f^{-1}(b)) = b \quad \text{for all } b \in B $$

 

The inverse "undoes" the effect of the original function.

 

 

Examples

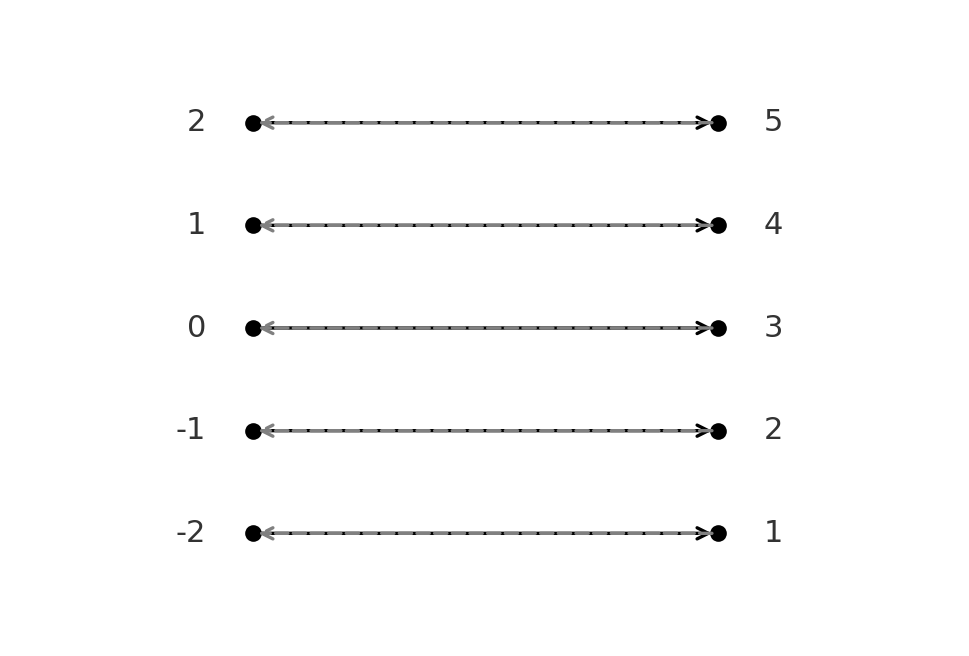
Bijective function: \( \large f(x)=x+3\) from \( \large \mathbb{Z} \to \mathbb{Z}\) is bijective.

 

The inverse function is \( \large f^{-1}(y)=y-3\).

 

 

Non-bijective function: \( \large f(x)=x^2\) from \( \large \mathbb{R} \to \mathbb{R}\) is not bijective, because it is not injective (both \( \large -2\) and \( \large 2\) give the image \( \large 4\)).

Therefore, no inverse function exists here.

 

 

Application

Bijective functions and their inverses play a central role in many areas of mathematics and computer science:

 

• Cryptography: Encryption algorithms require functions that can be uniquely reversed so messages can be decrypted again.
• Algebra: Isomorphisms between algebraic structures are bijections that preserve structure.
• Logic and theory: In mathematical proofs, bijections are used to compare the size of sets (cardinality).

 

Understanding bijective functions is therefore crucial for both theoretical and practical applications.