Examples of Functions
To better understand the properties of functions, we look here at concrete examples in the classical number sets: the natural numbers \( \large \mathbb{N}\), the integers \( \large \mathbb{Z}\), and the real numbers \( \large \mathbb{R}\).
Example 1: Injective function in \( \large \mathbb{N}\)
The function \( \large f : \mathbb{N} \to \mathbb{N}\) given by \( \large f(n) = 2n\).
$$ \large f(n) = 2n $$
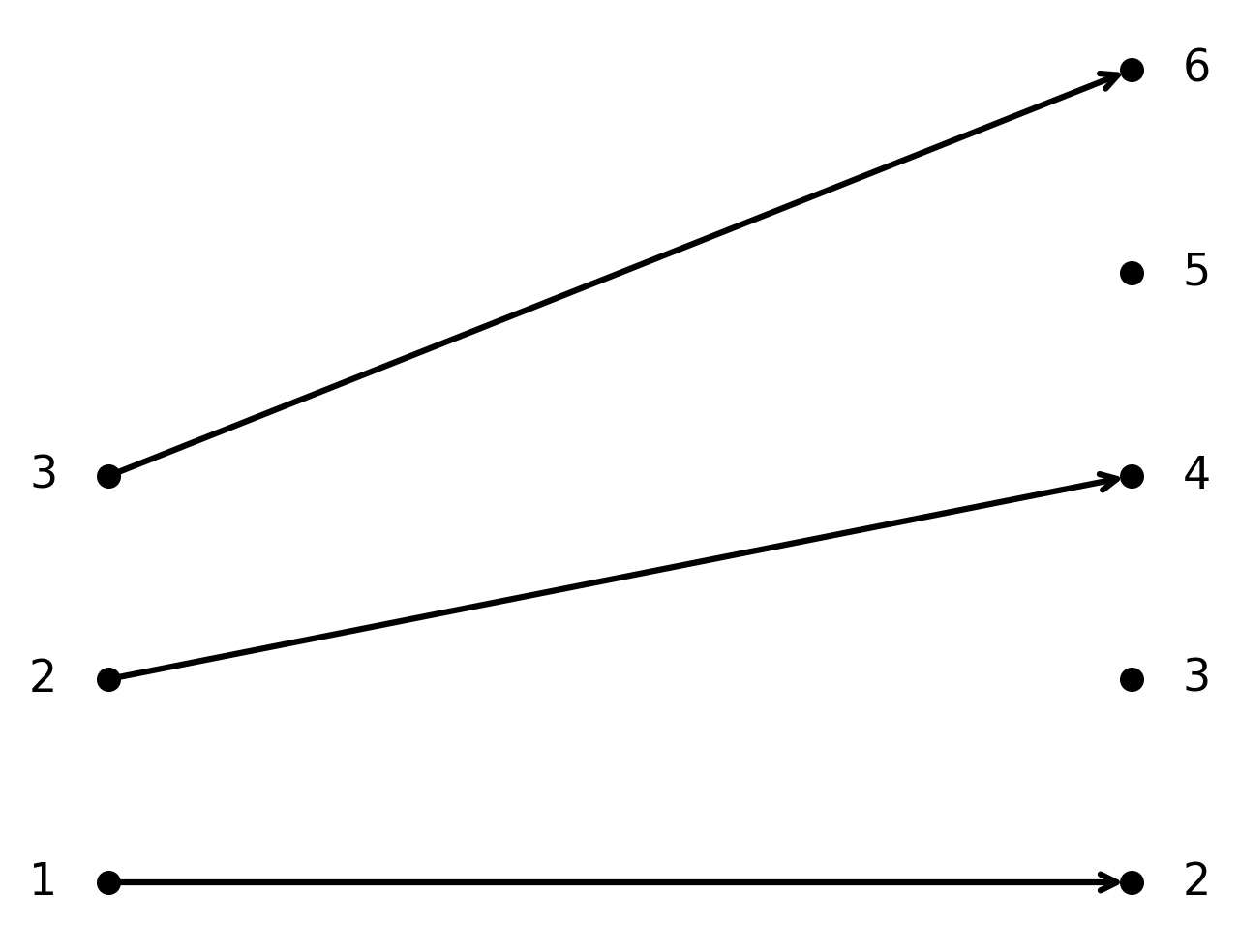
Here \( f\) is injective, because two different natural numbers always give different results when multiplied by 2. But the function is not surjective, since odd numbers are not hit.
Example 2: Surjective function in \( \large \mathbb{Z}\)
The function \( \large f : \mathbb{Z} \to \mathbb{Z}\) given by \( \large f(n) = \lfloor \frac{n}{2} \rfloor\).
$$ \large f(n) = \left\lfloor \frac{n}{2} \right\rfloor $$
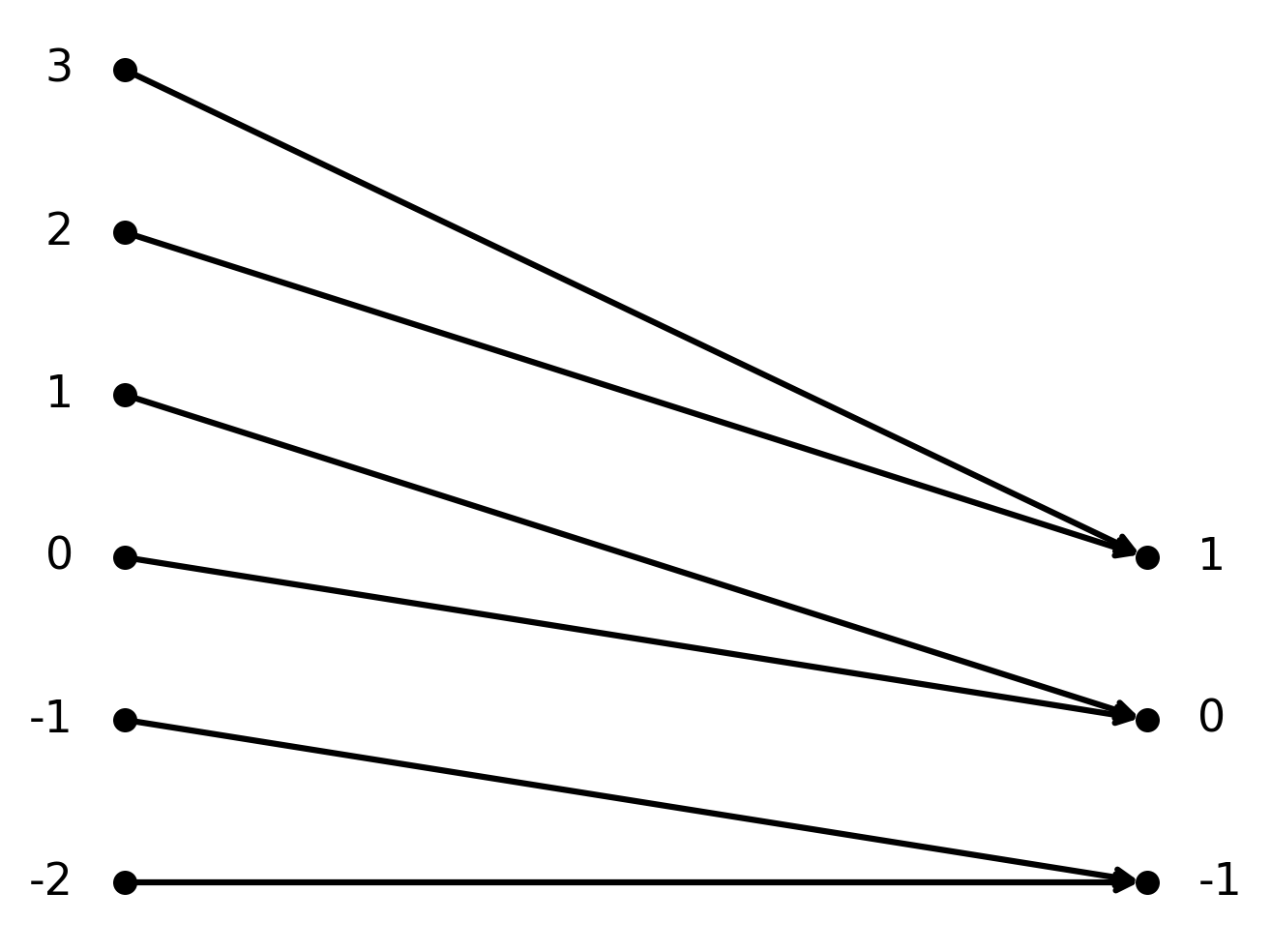
Here the function is surjective, because every integer is hit by at least one \( \large n\). For example, \(\large f(2)=1\) and \(\large f(3)=1\).
On the other hand, the function is not injective, because several inputs can give the same output.
Example 3: Bijective function in \( \large \mathbb{Z}\)
The function \( \large f : \mathbb{Z} \to \mathbb{Z}\) given by \( \large f(n) = n+1\).
$$ \large f(n) = n+1 $$

Here \(\large f\) is bijective: each integer gets a unique output, and all integers are hit.
Thus, the function can be inverted with an inverse \(\large f^{-1}(n) = n-1\).
Example 4: Functions in \( \large \mathbb{R}\)
In the real numbers, we can find many functions that illustrate the properties:
- \( \large f(x) = x^3 \) from \( \large \mathbb{R} \to \mathbb{R}\) is bijective. Every real number has a unique image, and the whole \( \large \mathbb{R}\) is covered.
- \( \large f(x) = x^2 \) from \( \large \mathbb{R} \to \mathbb{R}\) is not injective (because \( f(2)=f(-2)\)), but it is surjective if we only consider \( \large [0,\infty[\) as the codomain.
- \( \large f(x) = e^x \) from \( \large \mathbb{R} \to (0,\infty)\) is bijective, because all positive real numbers are hit uniquely.
Summary
The examples show that the properties of functions depend on:
- Which sets we consider as domain and codomain.
- How the function links input and output.
The classical number sets \( \large \mathbb{N}, \mathbb{Z}, \mathbb{R}\) provide many good and simple examples of injective, surjective, and bijective functions.