Advanced methods

Once you have learned the basic rules of differentiation, a new world of possibilities opens up. Many functions cannot be written directly as \( \large y = f(x) \), yet they can still be differentiated using extended methods. The three most important techniques are implicit differentiation, parametric differentiation, and the derivative of inverse functions.

 

 

Implicit differentiation

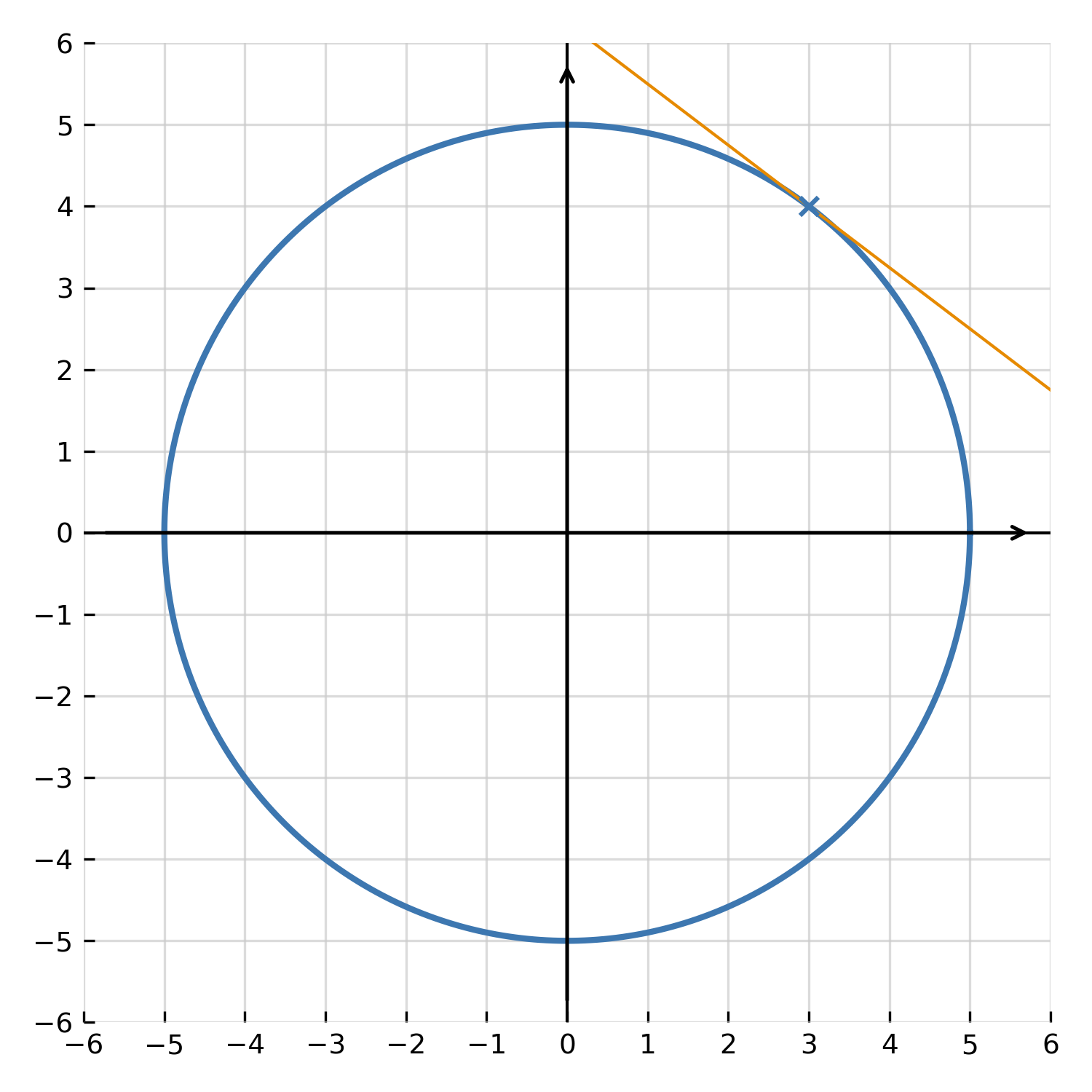
Some functions are given by an equation where \( \large x \) and \( \large y \) appear together, for example \( \large x^2 + y^2 = 25 \). One cannot isolate \( \large y \) directly, but it is possible to find \( \large \frac{dy}{dx} \) by differentiating both sides with respect to \( \large x \), remembering that \( \large y \) itself depends on \( \large x \).

 

Example:

 

Differentiate \( \large x^2 + y^2 = 25 \) with respect to \( \large x \):

 

$$ \large 2x + 2y \cdot \frac{dy}{dx} = 0 $$

 

Solve for \( \large \frac{dy}{dx} \):

 

$$ \large \frac{dy}{dx} = -\frac{x}{y} $$

 

This is the slope of the tangent to the circle \( \large x^2 + y^2 = 25 \) at any point. Implicit differentiation is especially useful for curves that cannot be described as functions in the traditional sense, such as circles, ellipses, and hyperbolas.

 

The chain rule in practice

The chain rule is used when a function consists of another function. It is central to all extended methods. One can think of it as “one change affecting another change.”

 

Example:

 

If \( \large y = \sin(3x^2) \), the function consists of two layers: \( \large \sin(u) \) where \( \large u = 3x^2 \). The derivative is found by multiplying the two rates of change:

 

$$ \large \frac{dy}{dx} = \cos(3x^2) \cdot 6x = 6x \cos(3x^2) $$

 

The chain rule can also be applied repeatedly, for example when a function is composed of three or more layers. It therefore becomes an indispensable tool in all advanced calculations.

 

 

Parametric functions

Sometimes both \( \large x \) and \( \large y \) are given as functions of a third variable, often called \( \large t \) (the parameter). This occurs, for example, in kinematics, where a particle moves through space and its position is known as a function of time.

 

If \( \large x = x(t) \) and \( \large y = y(t) \), one can find \( \large \frac{dy}{dx} \) by combining the two derivatives with respect to \( \large t \):

 

$$ \large \frac{dy}{dx} = \frac{\frac{dy}{dt}}{\frac{dx}{dt}} $$

 

Example:

 

If \( \large x = t^2 \) and \( \large y = 3t + 1 \), then

$$ \large \frac{dx}{dt} = 2t \qquad \text{and} \qquad \frac{dy}{dt} = 3 $$

 

Therefore,

$$ \large \frac{dy}{dx} = \frac{3}{2t} $$

 

This expression shows the slope of the curve at the point corresponding to the parameter \( \large t \).

 

 

Inverse functions

If a function has an inverse, it is also possible to find the derivative of the inverse without first determining it explicitly. Let \( \large y = f(x) \) be a differentiable function with an inverse \( \large x = f^{-1}(y) \). The relationship is:

 

$$ \large \frac{dy}{dx} = f'(x) \quad \Rightarrow \quad \frac{dx}{dy} = \frac{1}{f'(x)} $$

 

In other words, the derivative of the inverse function is the reciprocal of the derivative of the original function.

 

Example:

 

If \( \large f(x) = e^x \), then \( \large f^{-1}(x) = \ln(x) \). Since \( \large f'(x) = e^x \), it follows that:

 

$$ \large (\ln x)' = \frac{1}{e^x} = \frac{1}{x} $$

 

This matches the well-known derivative of the logarithm and demonstrates the principle in practice.

 

 

Combined methods

Often one encounters functions where several of these techniques must be used together — for example, an implicit equation involving a parameter, or a composite function that must be inverted. The experienced mathematician learns to combine the rules naturally:

 

$$ \large \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} $$

 

This is essentially an extended version of the chain rule, allowing one to switch between variables as needed.

 

 

Summary

The extended methods make it possible to differentiate functions that cannot be written in a simple form. Implicit differentiation is used for relationships between \( \large x \) and \( \large y \), parametric differentiation applies when both depend on a parameter, and the rule for inverse functions allows one to find derivatives of logarithmic and inverse trigonometric functions. These tools extend the scope of differential calculus and form the foundation for more advanced topics in analysis.