Vector types and roles

Vectors can have different roles depending on the context. Some are used to describe directions, others to indicate a perpendicular direction, or to form the basis for an entire coordinate system. Here we look at the most important types of vectors.

 

 

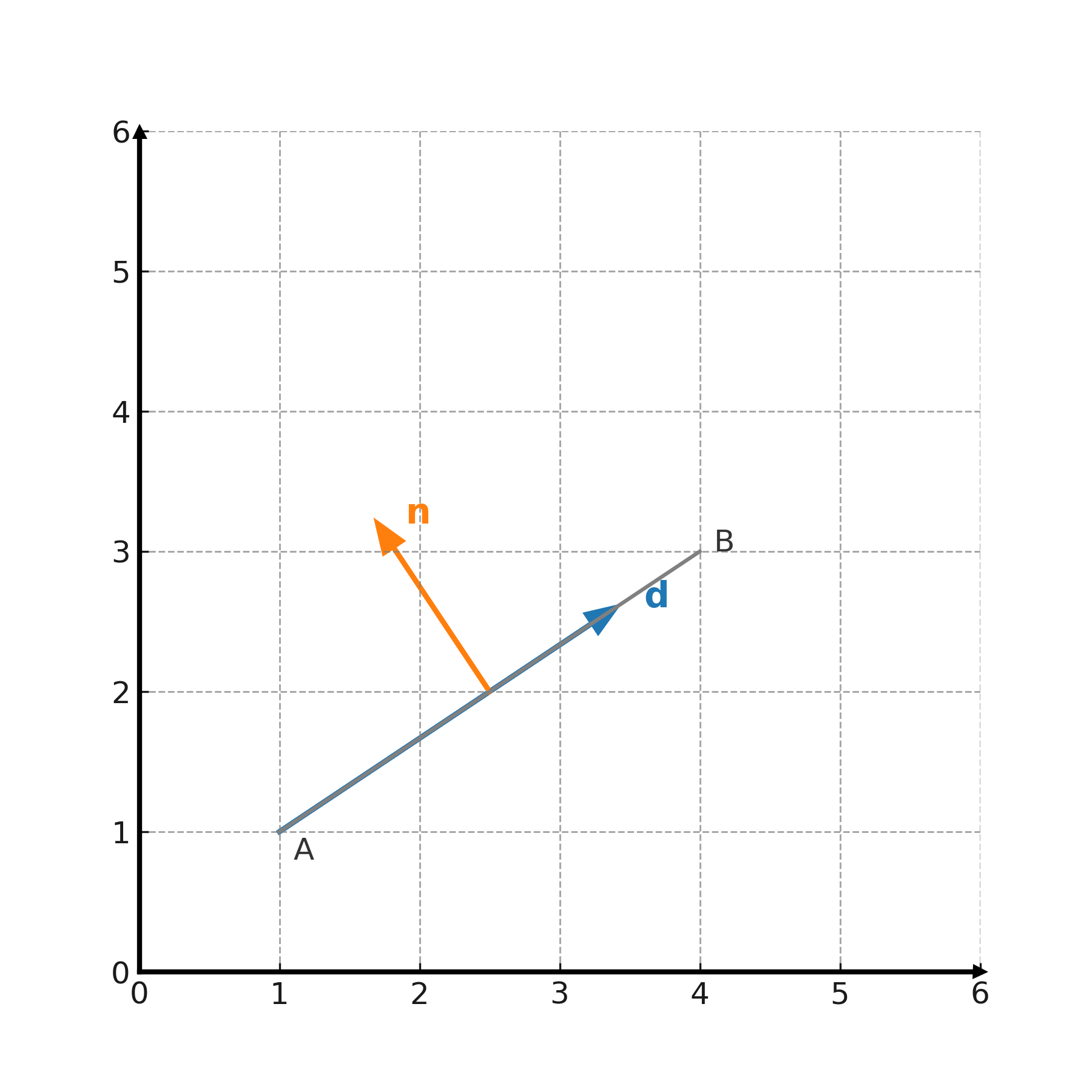
Direction vectors

A direction vector (d) describes the direction of a line or a plane. If a line passes through the points \( \large A=(x_1,y_1) \) and \( \large B=(x_2,y_2) \), then

 

$$ \large \mathbf{d} = (x_2-x_1,\; y_2-y_1) $$

 

is a direction vector for the line. With a direction vector one can write a parametric representation:

 

$$ \large (x,y) = (x_1,y_1) + t \cdot \mathbf{d}, \quad t \in \mathbb{R} $$

 

which describes all the points on the line.

 

 

Normal vectors

A normal vector is perpendicular to a line or a plane. If the line has direction vector \( \large (a,b) \), then

 

$$ \large \mathbf{n} = (-b,a) \quad \text{or} \quad (b,-a) $$

 

are normal vectors. A normal vector can be used to write a line in the form

 

$$ \large n_1 \cdot x + n_2 \cdot y + c = 0 $$

 

where \( \large (n_1,n_2) \) is the normal vector. That a vector is normal can be tested using the dot product: If \( \large \mathbf{r} \cdot \mathbf{n} = 0 \), then they are perpendicular.

 

 

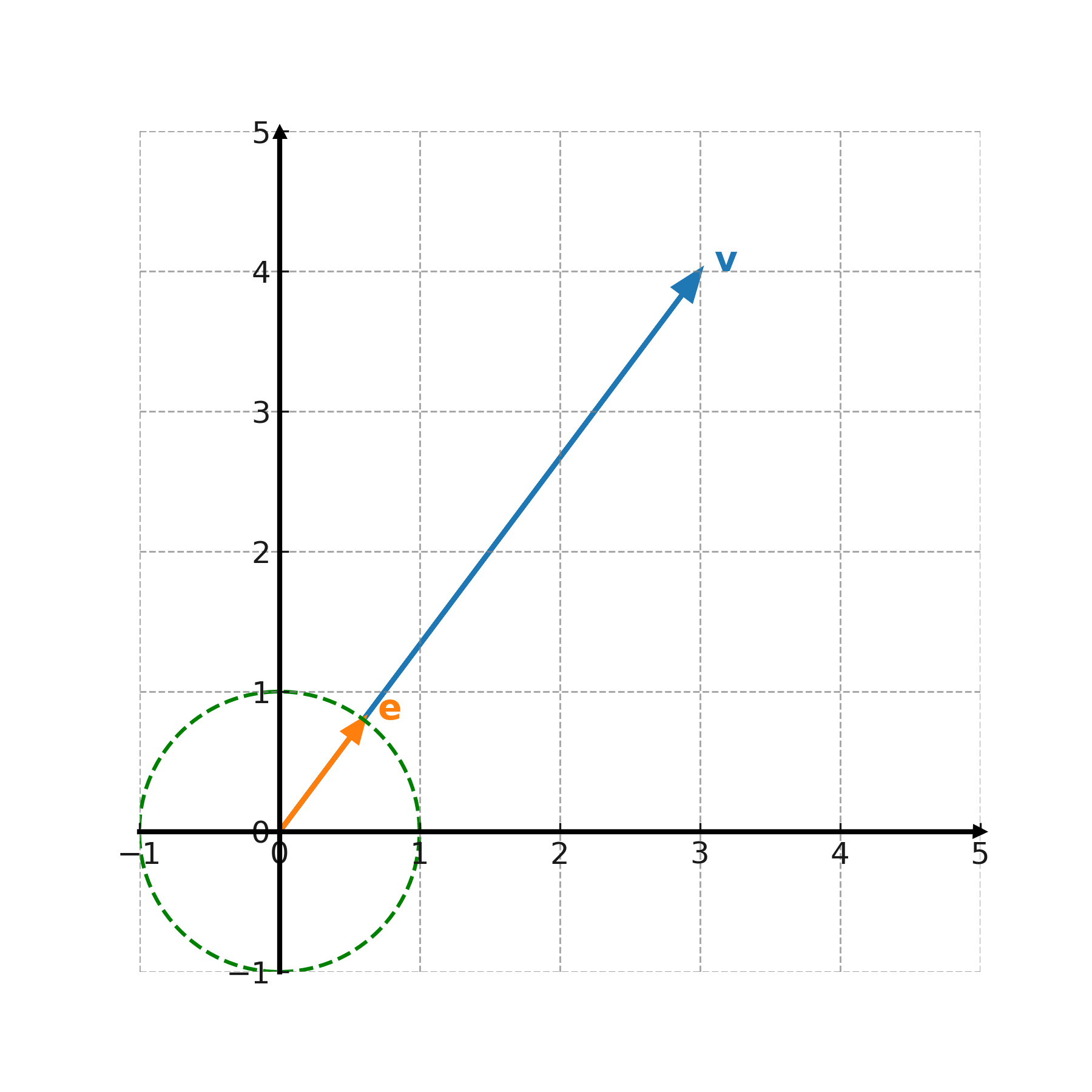
Unit vectors

A unit vector has length 1 and is used to describe a pure direction. Any vector can be made into a unit vector by dividing by its length:

 

$$ \large \mathbf{e} = \frac{1}{|\mathbf{v}|} \cdot \mathbf{v} $$

 

Unit vectors are used, for example, to define the directions of the axes in a coordinate system.

 

 

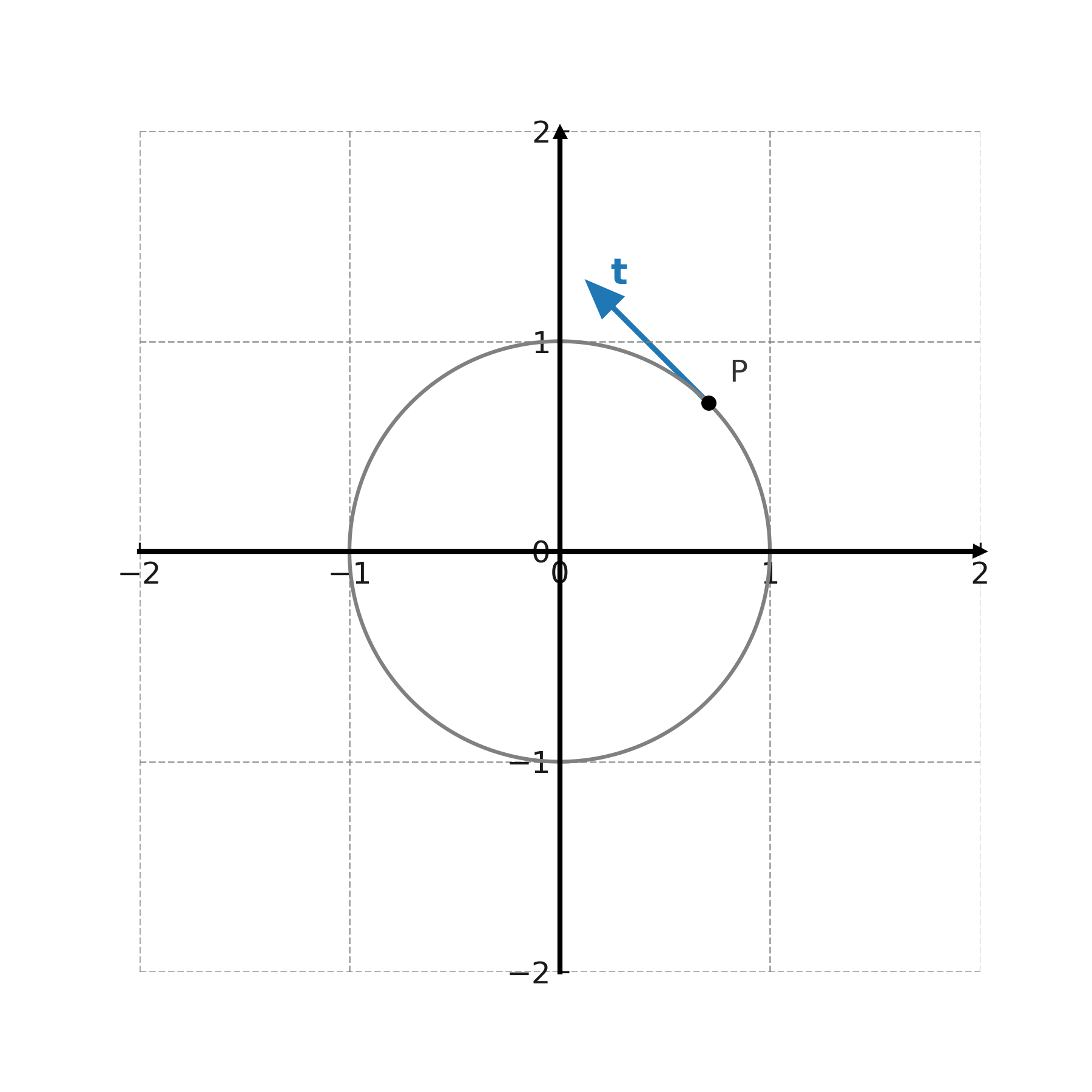
Tangent vectors

In the context of curves, tangent vectors are used to describe the direction at a given point. For a differentiable curve \( \large (x(t),y(t)) \), the tangent vector is given by

 

$$ \large \mathbf{t} = \big(x'(t),\,y'(t)\big) $$

 

which shows how the curve moves at the point.

 

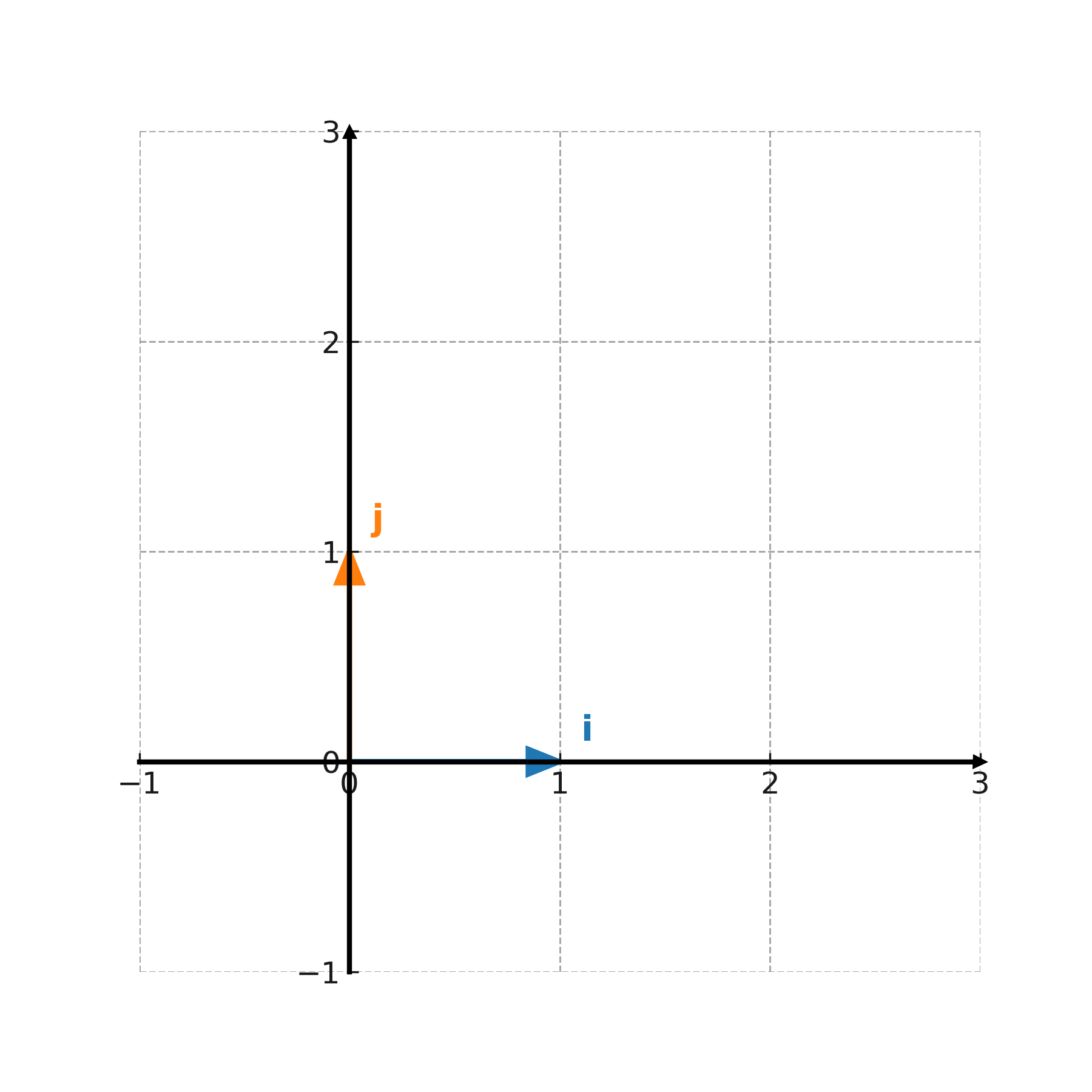
Basis vectors

In a coordinate system, basis vectors are used to describe all other vectors. In the plane, the standard basis is

 

$$ \large \mathbf{i} = (1,0), \quad \mathbf{j} = (0,1) $$

 

Every vector can be written as a combination of these: \( \large \mathbf{v} = x \cdot \mathbf{i} + y \cdot \mathbf{j} \).

 

Summary

Direction vectors are used to indicate directions of lines and planes, normal vectors to indicate perpendicular directions, unit vectors to isolate pure direction, tangent vectors to describe the course of curves, and basis vectors to build entire coordinate systems. Together they form the foundation of how vectors are applied in both geometry and algebra.