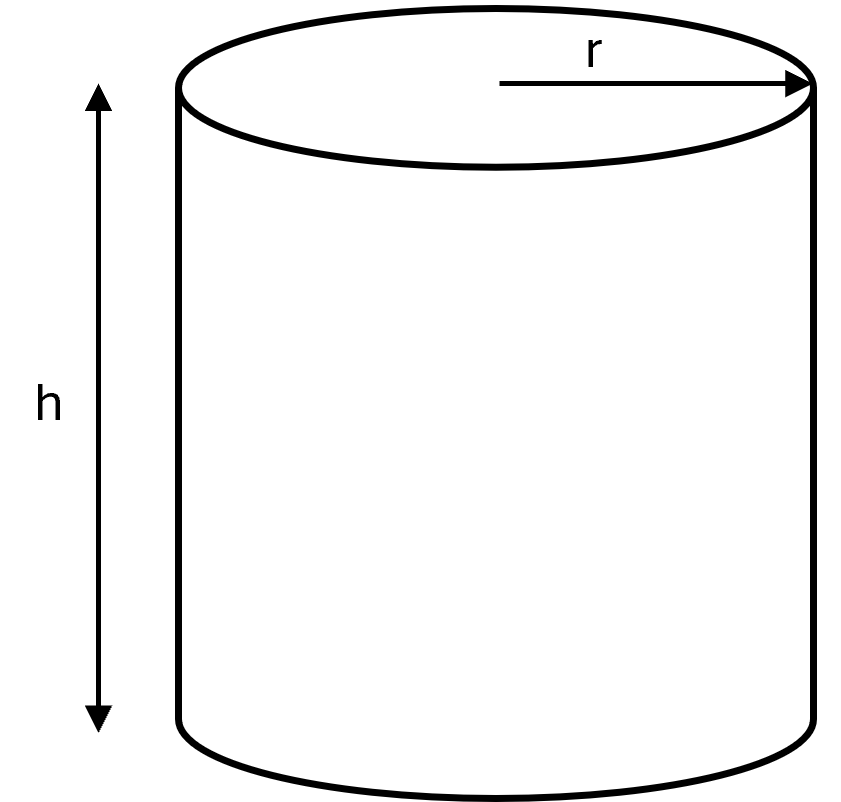
Cylinder
A cylinder is a three-dimensional figure consisting of two parallel circular bases and a curved lateral surface. The bases are congruent and are connected by the lateral surface.
A cylinder is called right if the lateral surface is perpendicular to the bases. If the lateral surface is slanted, it is called an oblique cylinder.
Volume
The volume of a cylinder is found by multiplying the area of the base by the height:
$$ \large V = A_{base} \cdot h $$
Since the base is a circle with radius \( \large r \), we get:
$$ \large V = \pi \cdot r^2 \cdot h $$
Surface area
The surface area consists of the two circular bases and the curved lateral surface. The lateral surface can be "unrolled" into a rectangle with height \( \large h \) and width equal to the circumference of the circle \( 2 \pi r \):
$$ \large S = 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h $$
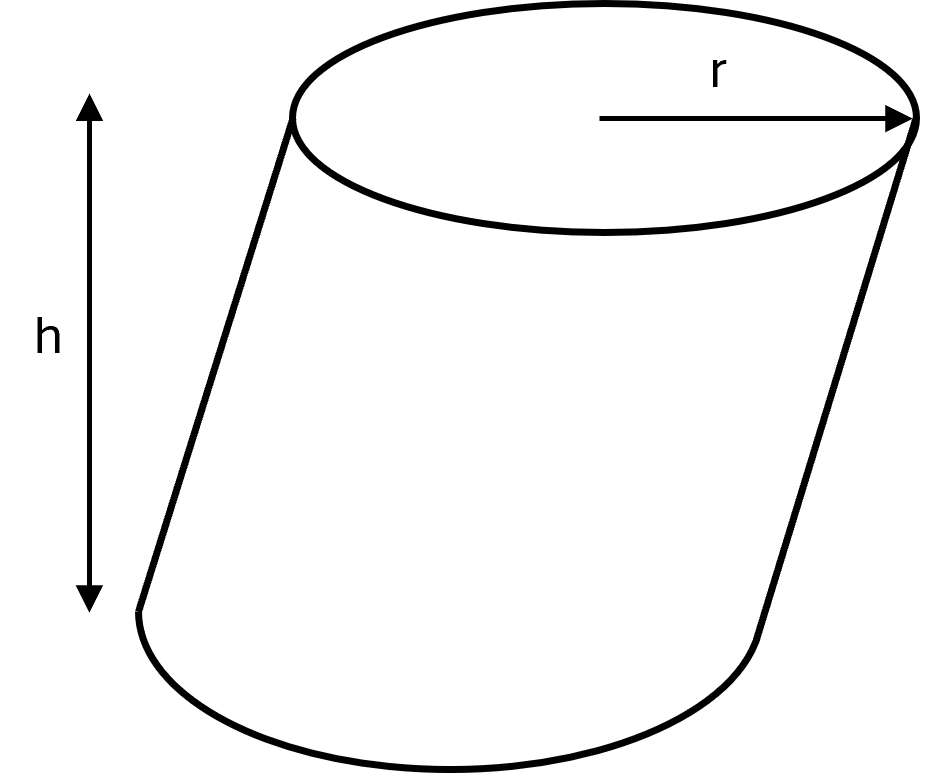
Oblique cylinder
In an oblique cylinder, the bases are still parallel and congruent, but the lateral surface is slanted.
The volume can still be found with the same formula, while the calculation of the surface area is more complicated and depends on the angle of the slant.
Truncated cylinder
A cylinder can also be cut by a plane that is not parallel to the bases. In this case, the upper surface becomes an ellipse instead of a circle.
The volume can still be calculated with the usual formula for the cylinder:
$$ \large V = \pi \cdot r^2 \cdot h $$
The surface area, however, is more complicated because the cross-section is an ellipse and the curved lateral surface is slanted.
There is no simple closed formula, and one typically has to use integral calculus or approximation methods to find it precisely.
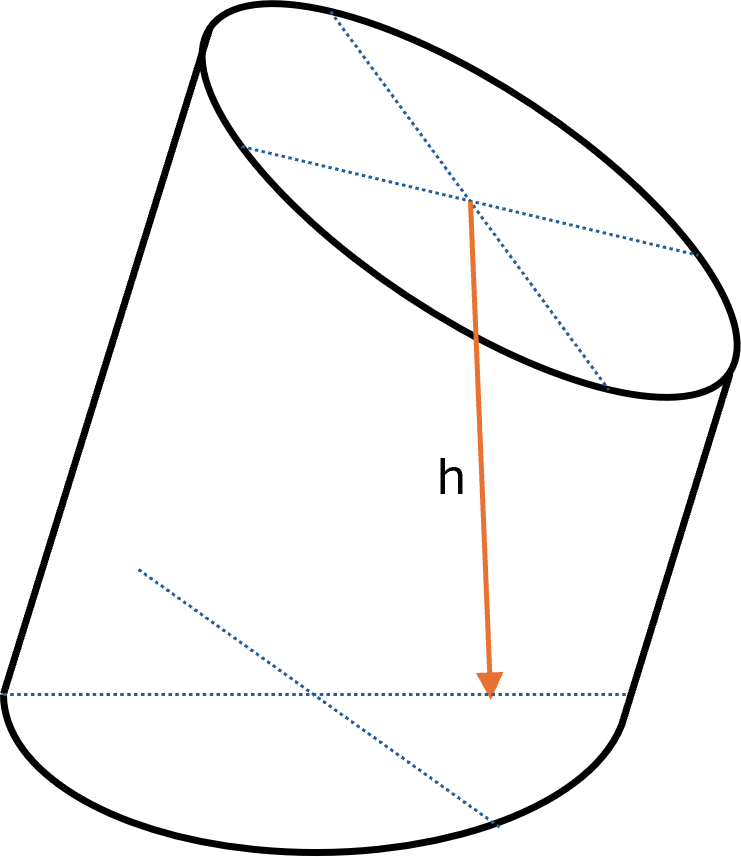
The height \( \large h \) is the perpendicular distance between the bottom and top planes.
Even though the top surface is slanted and the distance varies along the edge, the volume is always determined by this vertical height.