Subset, intersection and power set

An important part of set theory is comparing and combining sets. Here we look at subsets, proper subsets, intersections, power sets, and the Cartesian product.

 

Subset

A set \( \large A\) is a subset of another set \( \large B\) if all elements of \( \large A\) are also in \( \large B\). It is written as:

 

$$ \large A \subseteq B $$

 

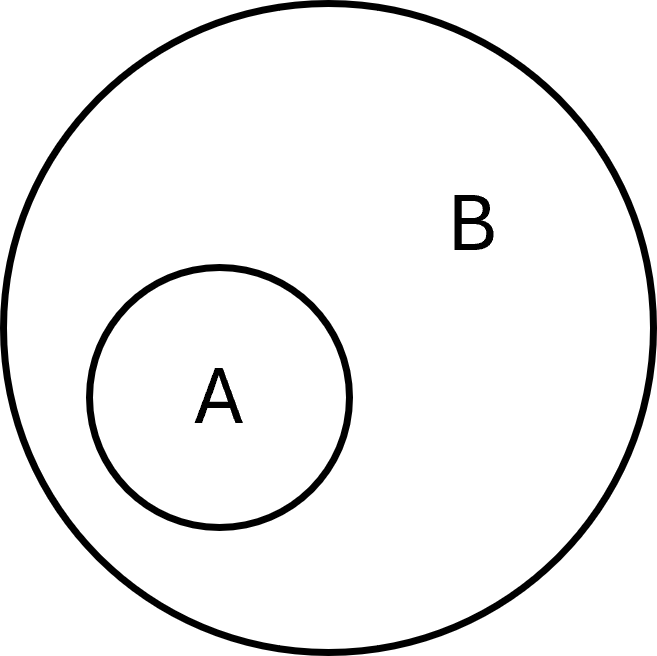
Subset

 

Formally, it can be defined as:

 

$$ \large A \subseteq B \;\;\Leftrightarrow\;\; \forall x \in A \Rightarrow x \in B $$

 

Examples:

 

  • \( \large \{1,2\} \subseteq \{1,2,3,4\}\)
  • The empty set is always a subset: \( \large \emptyset \subseteq A\) for any set \( \large A\).

 

Note: In some books the symbol \( \large \subset\) is used instead of \( \large \subseteq\) to denote subsets. Here we use \( \large \subseteq\) as the standard.

 

 

Proper subset

A set \( \large A\) is a proper subset of \( \large B\) if \( \large A \subseteq B\) but \( \large A \neq B\).

This means that \( \large B\) contains at least one element not in \( \large A\).

The notation is:

 

$$ \large A \subset B $$

 

Example: \( \large \{1,2\} \subset \{1,2,3\}\).

 

 

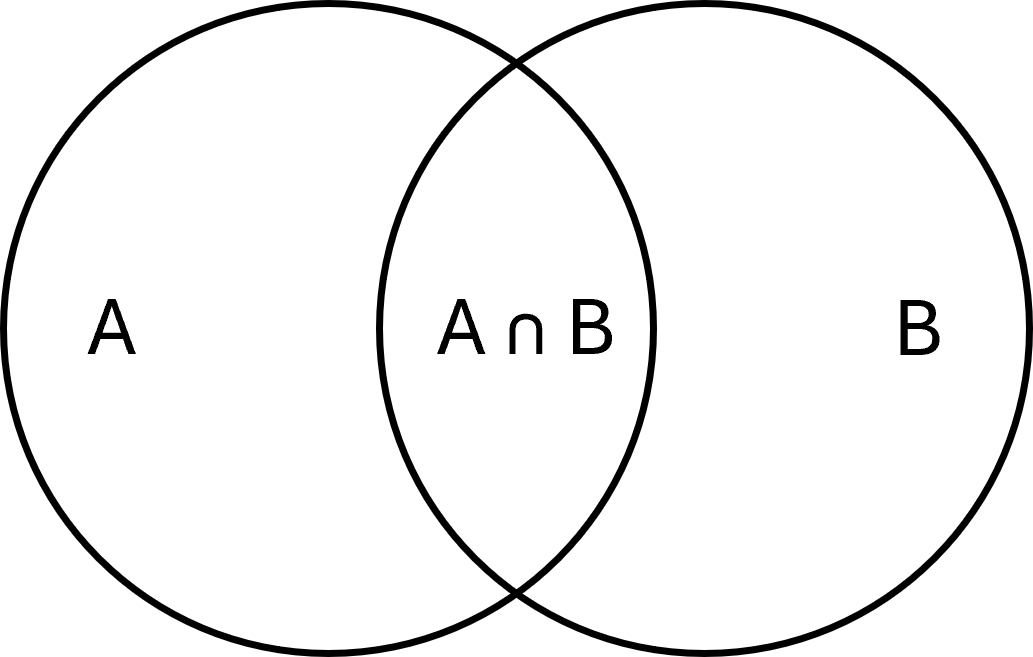
Intersection

The intersection of two sets \( \large A\) and \( \large B\) is the set of elements that are in both sets. It is written as:

 

$$ \large A \cap B = \{x \mid x \in A \;\wedge\; x \in B\} $$

 

Example: If \( \large A = \{1,2,3\}\) and \( \large B = \{3,4,5\}\), then \( \large A \cap B = \{3\}\).

 

 

Intersection

 

 

Power set

The power set of a set \( \large A\) is the set of all subsets of \( \large A\).

The power set is written as \( \large \mathcal{P}(A)\).

 

If \( \large A = \{0,1\}\), then:

 

$$ \large \mathcal{P}(A) = \{\emptyset, \{0\}, \{1\}, \{0,1\}\} $$

 

The number of elements in a power set is \( \large 2^{|A|}\).

For example, if \( \large |A| = 3\), then \( \large \mathcal{P}(A)\) has \( \large 2^3 = 8\) elements.

 

 

Cartesian product

The Cartesian product of two sets \( \large A\) and \( \large B\) is the set of all ordered pairs where the first component comes from \( \large A\) and the second component from \( \large B\).

It is written as:

 

$$ \large A \times B = \{(a,b) \mid a \in A \;\wedge\; b \in B\} $$

 

Example: If \( \large A = \{1,2\}\) and \( \large B = \{a,b\}\), then:

 

$$ \large A \times B = \{(1,a),(1,b),(2,a),(2,b)\} $$

 

Note that order matters: \( \large A \times B \neq B \times A\) in general.

 

 

 

 

Formulas

Logical symbols

$$ \begin{array}{rl} \forall & = \; \text{for all} \\[12pt] \exists & = \; \text{there exists} \\[12pt] \wedge & = \; \text{and} \\[12pt] \vee & = \; \text{or} \\[12pt] \neg & = \; \text{not} \\[12pt] \Rightarrow & = \; \text{if ... then} \\[12pt] \Leftrightarrow & = \; \text{if and only if} \end{array} $$

Notation

$$ \begin{array}{rl} a \in A & = \; \text{element $a$ is in the set $A$} \\[12pt] a \notin A & = \; \text{element $a$ is not in the set $A$} \\[12pt] A = B & = \; \text{$A$ is equal to $B$} \\[12pt] A \subseteq B & = \; \text{$A$ is a subset of $B$} \\[12pt] A \subset B & = \; \text{$A$ is a proper subset of $B$} \\[12pt] A \supseteq B & = \; \text{$A$ is a superset of $B$} \\[12pt] A \supset B & = \; \text{$A$ is a proper superset of $B$} \\[12pt] A \cup B & = \; \text{union of $A$ and $B$} \\[12pt] A \cap B & = \; \text{intersection of $A$ and $B$} \\[12pt] A \setminus B & = \; \text{difference of $A$ and $B$} \\[12pt] A^c & = \; \text{complement of $A$} \\[12pt] |A| & = \; \text{cardinality of $A$} \\[12pt] \varnothing & = \; \text{empty set} \end{array} $$