Continuity
When talking about the behavior of functions, one of the most important concepts is continuity. Continuity describes whether a function changes smoothly or whether jumps, holes or abrupt changes occur in the graph. A continuous function can be drawn without lifting the pencil from the paper.
Definition of continuity
A function \( \large f(x) \) is continuous at a point \( \large x = a \) if the limit of the function at that point equals the value of the function. It is written as:
$$ \large \lim_{x \to a} f(x) = f(a) $$
For a function to be continuous at a point, three conditions must be satisfied:
- The function is defined at \( \large a \)
- The limit \( \large \lim_{x \to a} f(x) \) exists
- The two values are equal
If even one of these conditions is not met, the function is not continuous at that point.
Types of discontinuity
There are several different ways a function can be non-continuous (discontinuous). The main types are:
| Type | Description |
|---|---|
| Jump discontinuity | The function suddenly jumps from one value to another. |
| Hole | The limit exists, but the function is not defined at the point. |
| Infinite discontinuity | The function grows without bound at the point (for example, near a vertical asymptote). |
These types can clearly be seen on the graph and help to understand the overall behavior of the function. The example below shows a jump discontinuity:
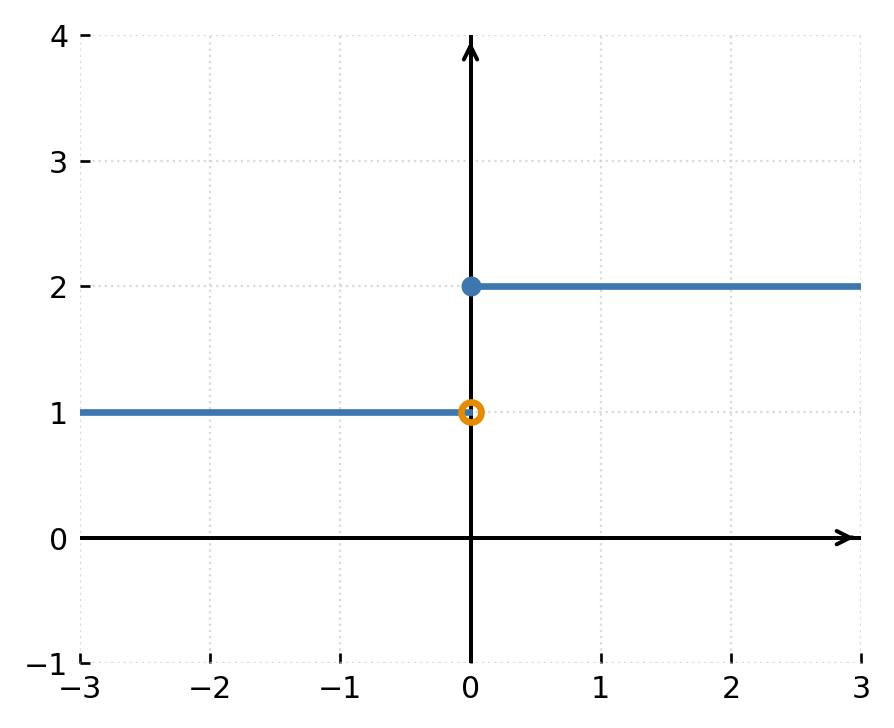
Examples
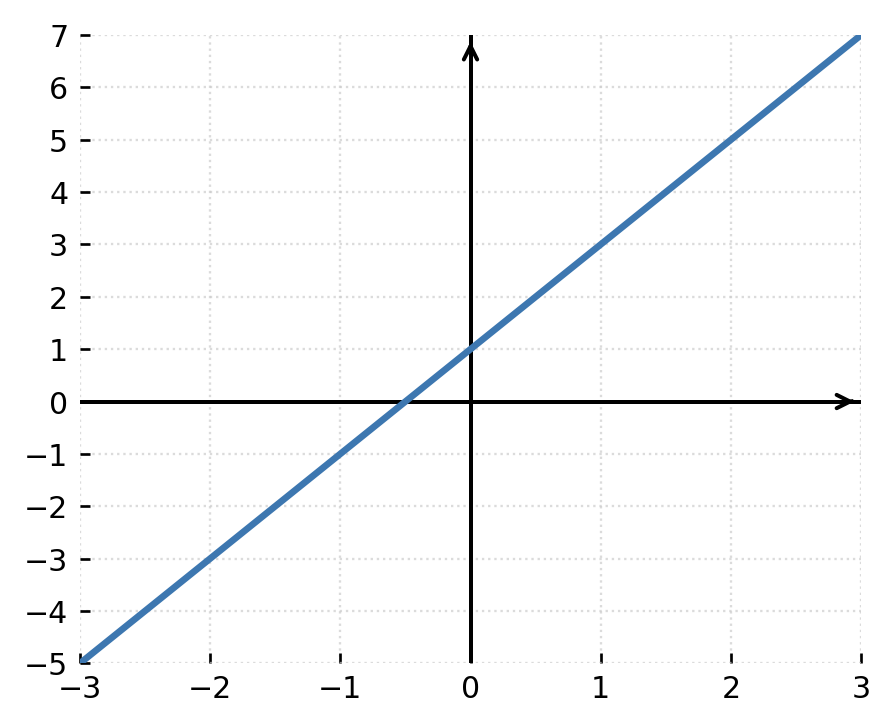
1: The function \( \large f(x) = 2x + 1 \) is continuous everywhere, because any value of x can be inserted without breaking the graph.
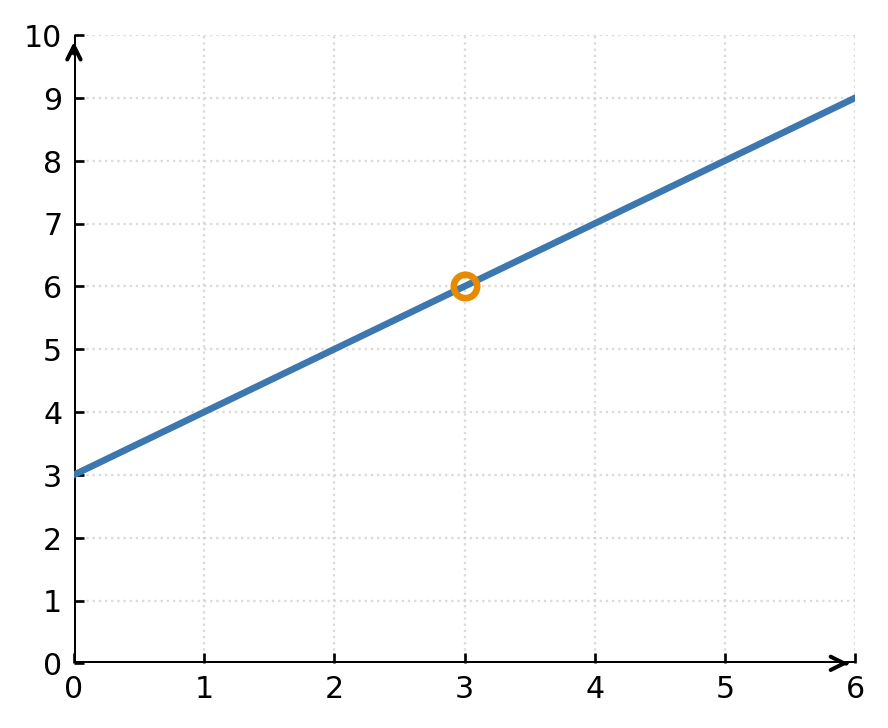
2: The function
$$ \large f(x) = \frac{x^2 - 9}{x - 3} $$
is not defined at \( \large x = 3 \), but the limit at that point exists:
$$ \large \lim_{x \to 3} \frac{x^2 - 9}{x - 3} = 6 $$
The graph therefore has a hole at the point (3, 6). The function can be made continuous by defining \( \large f(3) = 6 \).
Continuity on an interval
A function is said to be continuous on an interval if it is continuous at every point of the interval. Polynomials, exponential, logarithmic and trigonometric functions are examples of functions that are continuous everywhere they are defined.
Continuity is an important prerequisite for many theorems in analysis, including the intermediate value theorem and theorems on differentiability.
Importance in analysis
Continuity ensures that small changes in x lead to small changes in f(x). This property is essential for defining the derivative, which describes the slope of the function and its local changes. Continuity is therefore a fundamental building block of all analysis.