Definite integral

The definite integral is used to calculate the total quantity of a function between two points. While the indefinite integral describes all antiderivatives, the definite integral gives a number representing the accumulated value — often an area.

 

 

Definition

The definite integral of a function \( \large f(x) \) from \( \large a \) to \( \large b \) is defined as the limit of the sum of many small rectangles under the graph:

 

$$ \large \int_a^b f(x)\,dx \;=\; \lim_{n \to \infty} \sum_{i=1}^{n} f(x_i)\,\Delta x $$

 

Each term in the sum represents the area of a small rectangle with height \( \large f(x_i) \) and width \( \large \Delta x \). As the number of rectangles increases, the approximation becomes more precise, and in the limit, the exact area is obtained.

 

 

Geometric interpretation

If \( \large f(x) \ge 0 \) on the interval, the definite integral represents the area between the graph and the x-axis. If the function crosses the x-axis, the regions below the axis are counted as negative, so the integral shows the net area.

 

 

 

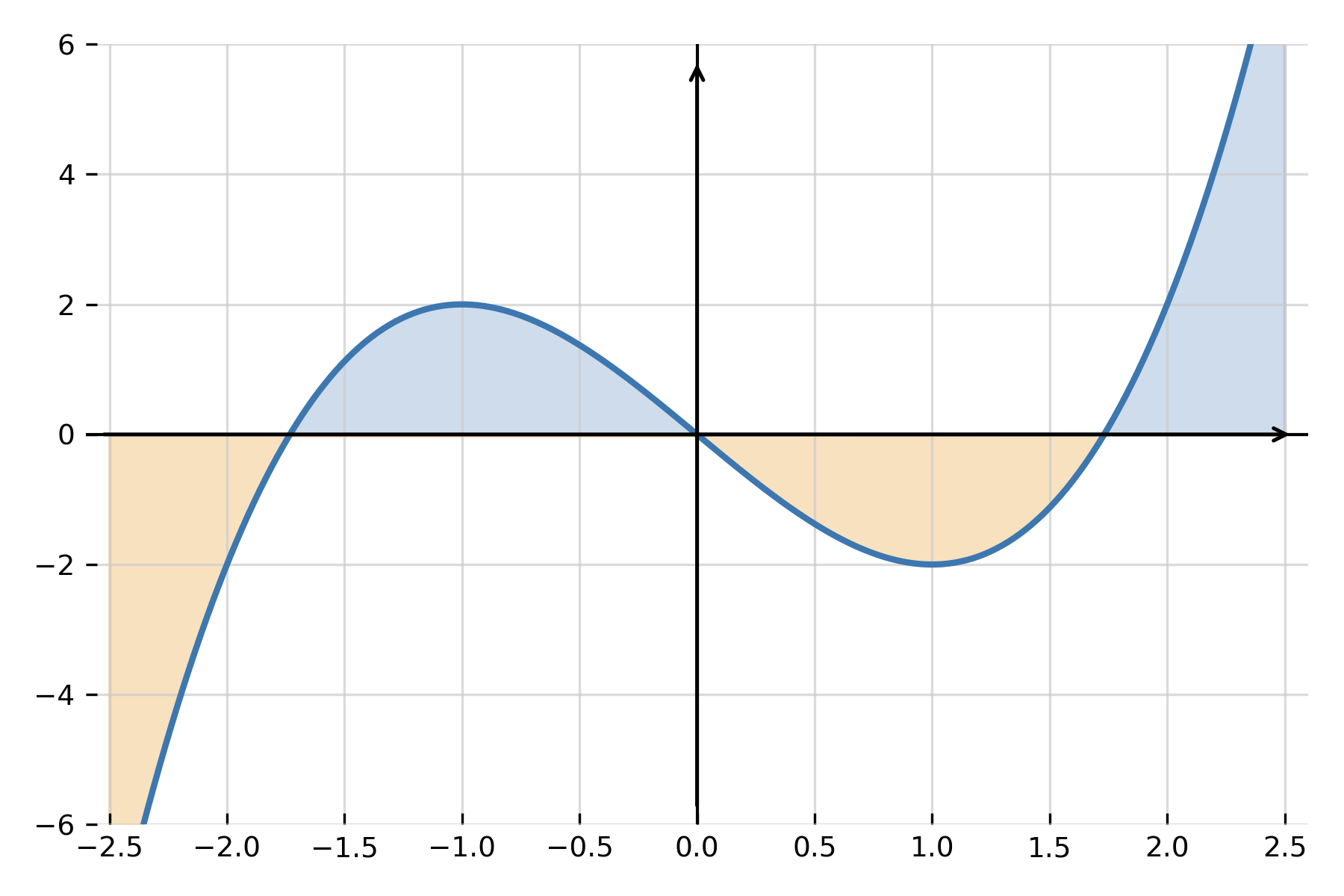
Fundamental theorem

There is a close connection between antiderivatives and definite integrals. If \( \large F \) is an antiderivative of \( \large f \), the fundamental theorem of calculus states:

 

$$ \large \int_a^b f(x)\,dx \;=\; F(b) - F(a) $$

 

This means that a definite integral can be found without computing Riemann sums. Instead, one finds an antiderivative and subtracts the function values at the two limits.

 

 

Example 1: Area under the graph

Find the area under \( \large f(x) = x^2 \) from \( \large x=0 \) to \( \large x=3 \):

 

$$ \large \int_0^3 x^2\,dx \;=\; \Big[\tfrac{1}{3}x^3\Big]_0^3 \;=\; \tfrac{1}{3}\cdot 27 - 0 \;=\; 9 $$

 

The area under the graph is therefore 9 units.

 

 

Example 2: Negative and positive contributions

Find \( \large \int_{-1}^{2} (x-1)\,dx \):

 

$$ \large \int_{-1}^{2} (x-1)\,dx \;=\; \Big[\tfrac{1}{2}x^2 - x\Big]_{-1}^{2} \;=\; \big(2 - 2\big) - \big(\tfrac{1}{2} - (-1)\big) = -\tfrac{3}{2} $$

 

The integral is negative because the function lies below the x-axis in part of the interval. The definite integral thus measures the net accumulation, not just the sum of positive areas.

 

 

Sign and accumulated quantity

A positive integral means that the function lies on average above the x-axis over the interval. A negative integral means the opposite. In physics and economics, this is interpreted as surplus or deficit in a total quantity.

 

 

Graphical interpretation

The definite integral can be understood as the sum of signed areas. It can therefore be visualized as the area between the graph and the x-axis, where areas below the axis are subtracted.

 

 

Summary

The definite integral gives a number representing the total change, accumulated quantity, or net area of a function between two limits. It can be found either geometrically as an area or algebraically via antiderivatives and the fundamental theorem.